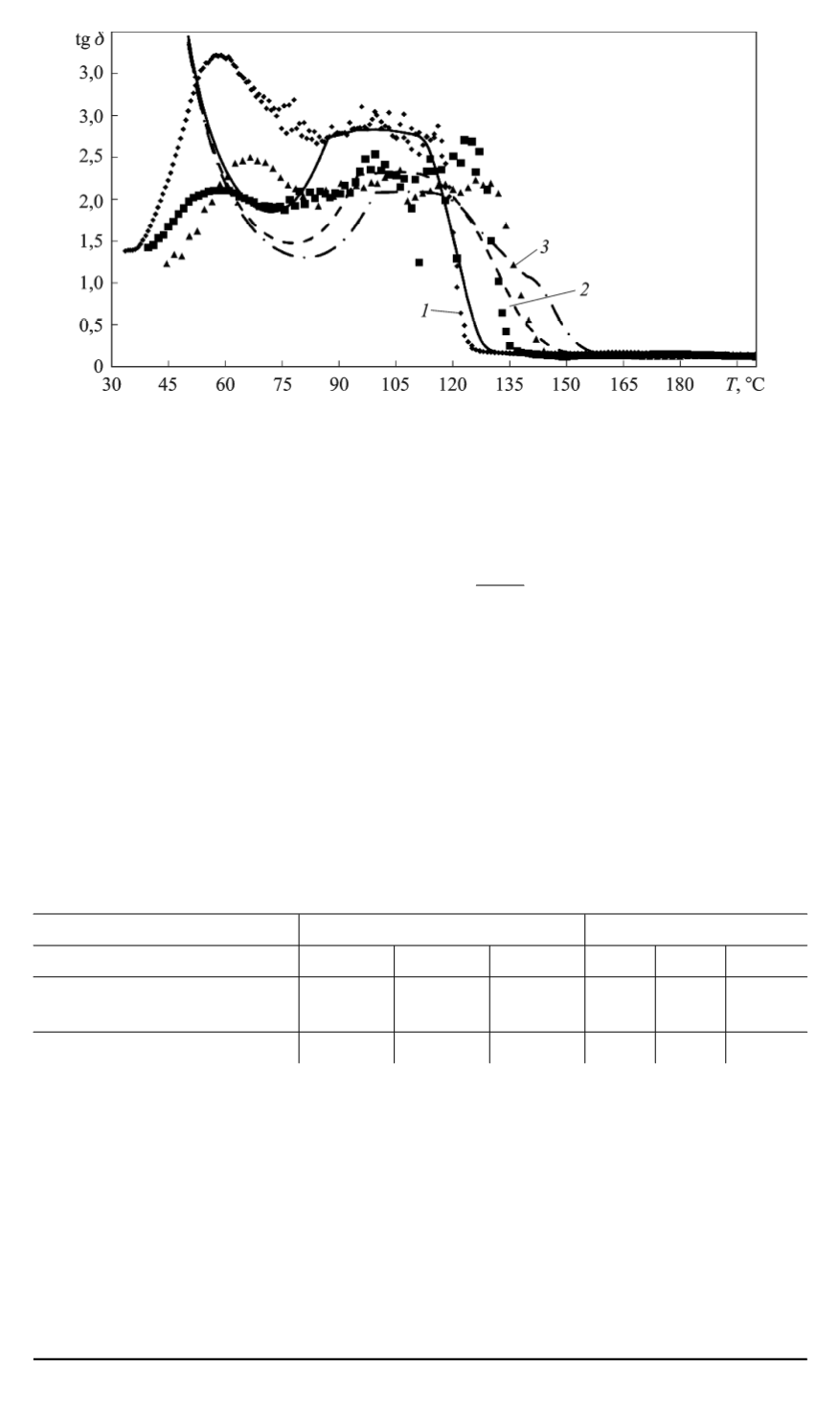
Рис. 3. Зависимость тангенса механических потерь tg
δ
от температуры
T
при нагревании с постоянной скоростью 1, 2, 3
◦
C/мин (кривые
1, 2, 3
соответственно). Точки на графике — экспериментальные данные, линии —
рассчитанные по предложенной модели (10)
функциональной зависимости
tg
δ
(
α
)
используется математическая модель
tg(
T, α
) =
ξ
(
α
)
e
ϑ
(
α
)
RT
(
t
)
,
(10)
где
ξ
(
α
)
и
ϑ
(
α
)
определяются аналогично функциям
η
∞
(
α
)
и
E
μ
(
η
)
.
Сравнительные данные эксперимента по исследованию тангенса угла ме-
ханических потерь в процессе отверждения препрега на трех скоростях на-
грева и расчета значений тангенса угла механических потерь по уравнению
(10) приведены на рис. 3.
Сравнительные результаты проведения экспериментов по исследованию
реологии процесса отверждения препрега методом ДМА и расчета по урав-
нению (10) показаны в табл. 2.
Таблица 2
Анализ результатов проведения вязкостного эксперимента и расчета
координаты точки гелеобразования
Параметры отверждения Экспериментальные данные Расчетные данные
Скорость нагрева,
◦
С/мин
1
2
3
1
2
3
Температура точки ге-
леобразования
T
gel
,
◦
С
121
132
137 123 133 141
Степень отверждения
α
0,163 0,182 0,179 0,183 0,177 0,190
В реальном производстве композитов используются ступенчатые темпе-
ратурно-временные режимы отверждения. Один из них предусматривает на-
грев со скоростью 2
◦
С/мин до температуры 60
◦
С, выдержку при заданной
температуре 1 ч, нагрев со скоростью 2
◦
С/мин до температуры 165
◦
С, вы-
держку при заданной температуре 6 ч.
Проведен эксперимент по определению кинетики и реологии отвержде-
ния препрега по рассмотренному режиму. Сравнительные результаты прове-
дения эксперимента и расчета по системе уравнений (9) степени отверждения
α
и комплексной вязкости
η
приведены на рис. 4.
Реализация алгоритмов решения поставленных задач организована на ба-
зе математического пакета Mathematica 7.0 компании Wolfram Research.
118 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2011. № 1


