Аррениуса–Френкеля–Эйринга [17]:
ln [
η
(
T, α
)] = ln [
η
∞
(
α
)] +
E
η
(
α
)
RT
(
t
)
,
(8)
где
η
∞
(
α
)
, Па
∙
с, — предельное значение вязкости при
T
→ ∞
;
E
η
(
α
)
, кДж/моль,
— энергия активации вязкого течения.
С учетом уравнений (1), (2), (7), (8) система (6) принимает следующий
вид:
dα
dT
β
=
A
(
α
)
e
−
E
a
(
α
)
RT
(1
−
α
)
n
;
ln [
η
(
T, α
)] = ln [
η
∞
(
α
)] +
E
η
(
α
)
RT
(
t
)
.
(9)
Большинство параметров, входящих в систему уравнений (9), не явля-
ются константами, а представляют собой функции температуры
T
, степени
отверждения
α
или времени
t
. Решить такую систему уравнений можно толь-
ко численно.
Неизвестные функции
A
(
α
)
и
E
a
(
α
)
системы (9) находятся с помощью
метода наименьших квадратов. Дифференциальное уравнение кинетики ре-
шается методом Рунге–Кутты четвертого порядка точности. Неизвестные
функции
η
∞
(
α
)
и
E
μ
(
η
)
системы (9) находятся методом наименьших квадра-
тов, совмещением вязкостного эксперимента, проведенного на определенной
скорости нагрева, с кривой изменения степени отверждения
α
на той же
скорости нагрева, рассчитанной по макрокинетической модели (5).
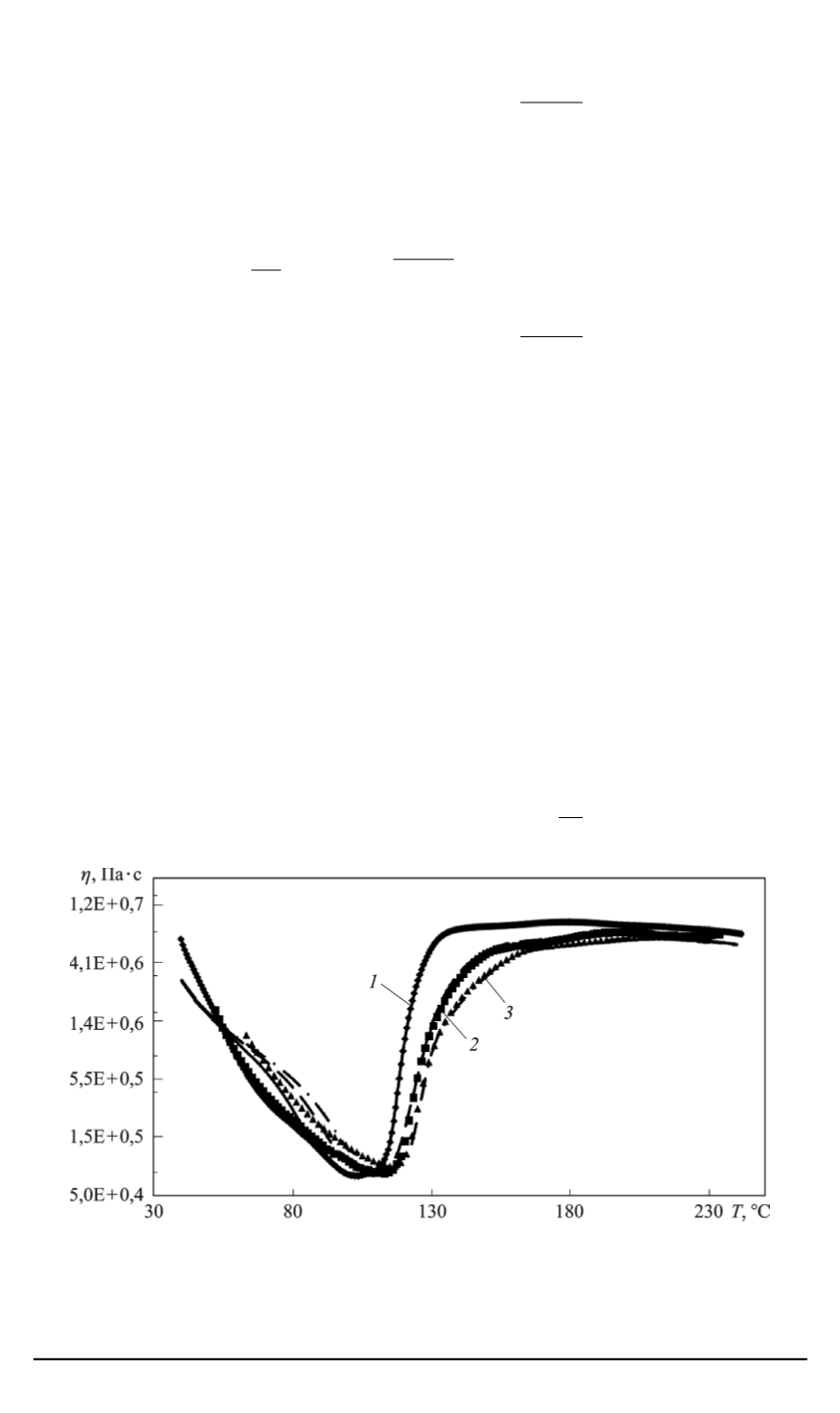
Сравнительные данные эксперимента по исследованию реологии отвер-
ждения препрега на трех скоростях нагрева и расчета значений вязкости по
системе уравнений (9) приведены на рис. 2.
Точка гелеобразования
T
gel
отверждающейся вязкой системы определяет-
ся при динамических вязкостных испытаниях из условия равенства единице
тангенса угла механических потерь в соответствии с работой [9]. Тангенс
угла механических потерь определяется как
tg
δ
=
η
0
η
00
[18]. Для построения
Рис. 2. Зависимость комплексной вязкости
η
от температуры
T
,
◦
С, при
отверждении препрега на трех скоростях нагрева 1, 2, 3
◦
C/мин (кривые
1, 2,
3
соответственно). Точки на графике — экспериментальные данные, линии —
расчетные, по предложенной модели (9)
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2011. № 1 117


