Таблица 1
Результаты расчета по модели (4) на основе экспериментальных данных
Число точек разбиения температурного интервала проведения
экспериментов
1000
Коэффициент детерминации RSquared
0,98
Предэкспоненциальный коэффициент
А
, мин
−
1
9
,
95
∙
10
9
Показатель реакции
n
1,41
Энергия активации
E
a
, кДж/моль
89,79
Анализ кинетики 36 различных партий препрегов на основе связую-
щего ЭНФБ и трех марок углеродного наполнителя арт. 3692, арт. 4510,
арт. 4500 на скоростях 1. . . 10
◦
С/мин позволяет утверждать, что линейная
модель (5) приемлема для моделирования кинетики отверждения препрега в
условиях нагрева с постоянной скоростью. Отклонение расчетных значений
степени отверждения от экспериментальных в области скоростей нагрева
1
◦
C/мин
6
β
6
3
◦
C/мин не превышает 3%, в области скоростей нагрева
3
◦
C/мин
< β
6
10
◦
C/мин не превышает 7%.
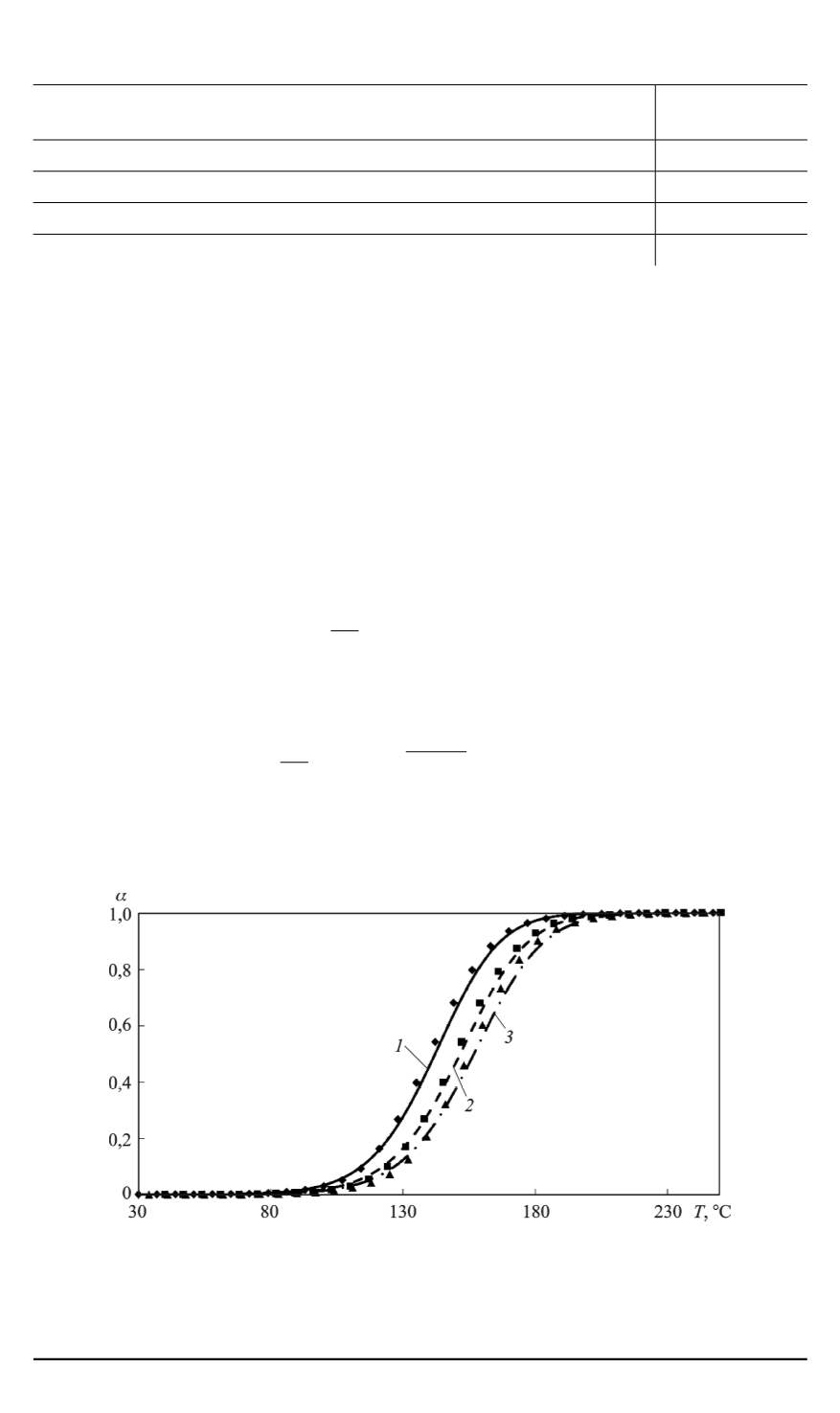
Сравнительные экспериментальные данные по исследованию кинетики
отверждения препрега на трех скоростях нагрева 1, 2, 3
◦
С/мин и расчета по
модели (5) приведены на рис. 1.
В обобщенной формулировке хемовязкостная модель для термореактив-
ной полимерной системы представляет собой связанную пару уравнений,
описывающих изменение степени отверждения
α
и вязкости
η
:
dα
dt
= Φ [
T
(
t
)
, α
] ;
η
=
η
[
T, α
]
.
(6)
Кинетика процесса отверждения препрега описывается уравнением вида
dα
dt
=
A
(
α
)
e
−
E
a
(
α
)
RT
(1
−
α
)
n
,
(7)
где
A
(
α
)
, мин
−
1
, — предэкспоненциальный коэффициент;
E
a
(
α
)
, кДж/моль,
— энергия активации.
Реология процесса отверждения препрега описывается уравнением типа
Рис. 1. Зависимость степени отверждения
α
от температуры
T
,
◦
С, при
отверждении препрега на трех скоростях нагрева 1, 2, 3
◦
С/мин (кривые
1, 2,
3
соответственно). Точки на графике — экспериментальные данные, линии —
расчетные по предложенной модели (5)
116 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2011. № 1


