
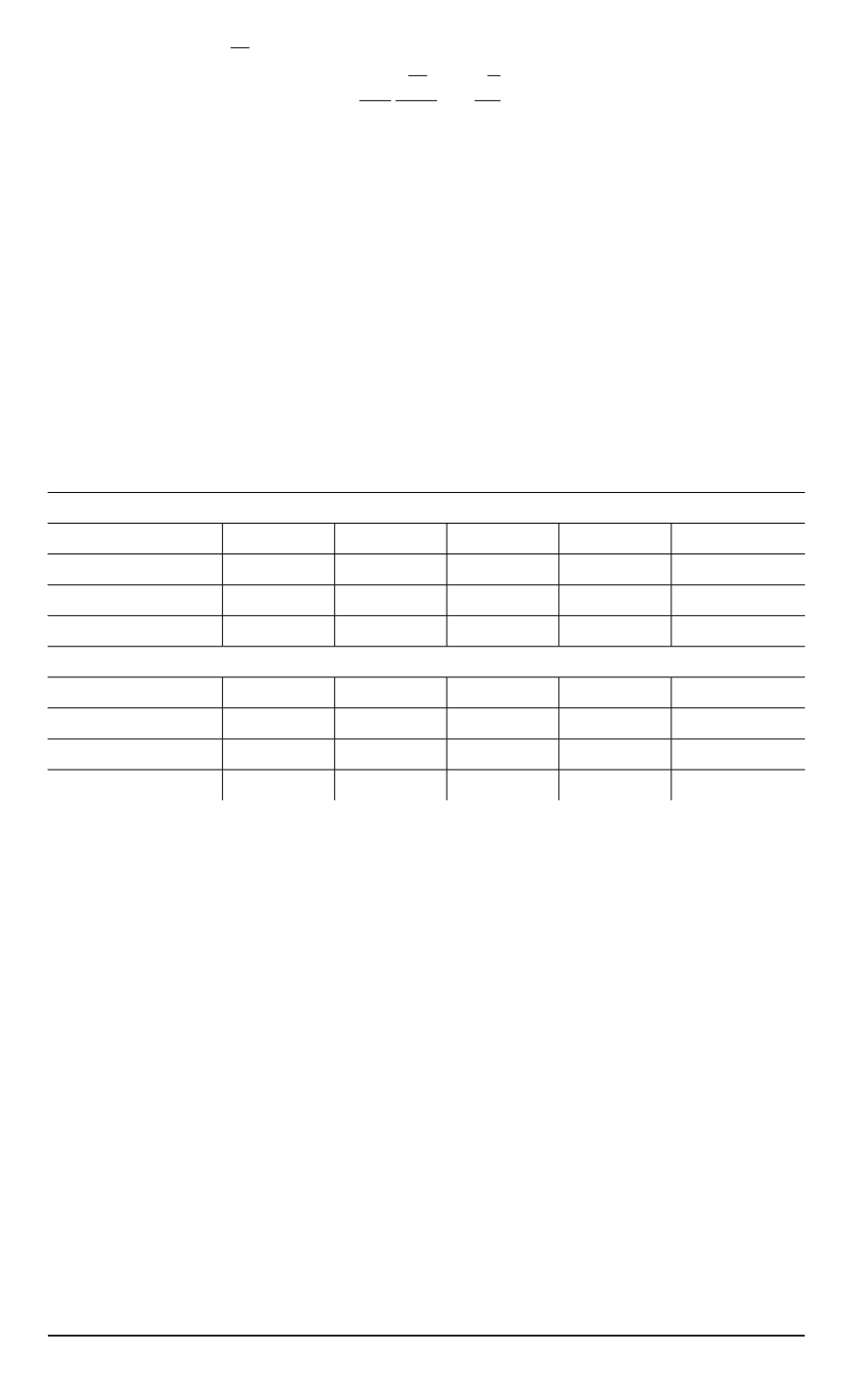
скорости потока
w
:
λ
1
d
гм
ρw
2
2
=
dp
dz
.
(3)
Использование указанных определяющих параметров в численных
расчетах и в экспериментах дает лучшую аппроксимацию результа-
тов по сравнению с другими возможными.
Экспериментальные значения стабилизированных КГС трения в
моделях ТВС, полученные по аппроксимациям измерений статическо-
го давления на двух смежных гранях чехла, приведены в табл. 2. По-
грешности экспериментального определения КГС составили 6. . . 8%.
Значительный вклад в погрешности вносят неопределенности геоме-
трических размеров моделей, в первую очередь чехла.
Таблица 2
Значения КГС трения
Модель № 1 центральной части активной зоны
Re
5,79
∙
10
4
5,16
∙
10
4
4,47
∙
10
4
3,81
∙
10
4
3,13
∙
10
4
Эксперимент
0,0247
0,0253
0,0261
0,0273
0,0279
Расчет по (2)
0,0269
0,0276
0,0287
0,0298
0,0313
Отклонение, % – 8,7
– 9,3
– 9,8
– 9,2
– 12,3
Модель № 2 периферийной части активной зоны
Re
6,06
∙
10
4
5,56
∙
10
4
4,87
∙
10
4
4,18
∙
10
4
3,33
∙
10
4
Эксперимент
0,0267
0,0269
0,0278
0,0285
0,0293
Расчет по (2)
0,0259
0,0264
0,0273
0,0284
0,0301
Отклонение, % 3,1
1,7
1,7
0,3
– 2,6
Данные табл. 2 могут быть представлены в виде
λ
ц
= 0
,
379
Re
−
0
,
25
±
±
2
%,
λ
п
= 0
,
410
Re
−
0
,
25
±
3%, где
λ
ц
и
λ
п
— коэффициенты сопротив-
ления трения моделей центральной и периферийной частей активной
зоны.
Сравнение результатов экспериментов с зависимостью (2) дает
среднеквадратическое отклонение 9,9% для модели № 1 и 2,1% для
модели № 2 при предельных отклонениях 12,3% и 3,1% соответ-
ственно.
Отметим, что расчетное значение коэффициента гидравлического
сопротивления трения пучка гладких стержней, расположенных с от-
носительным шагом 1,325, при числе Рейнольдса 7,3
∙
10
4
составляет
0,0211 и на 3% меньше значения, полученного по эмпирической кор-
реляции ФЭИ [6].
Экспериментальное и расчетное распределения продольной скоро-
сти потока вдоль осевой линии зазора между первым (проходящим
через ось моделей) и вторым слоями имитаторов твэлов приведены на
88 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 1

















