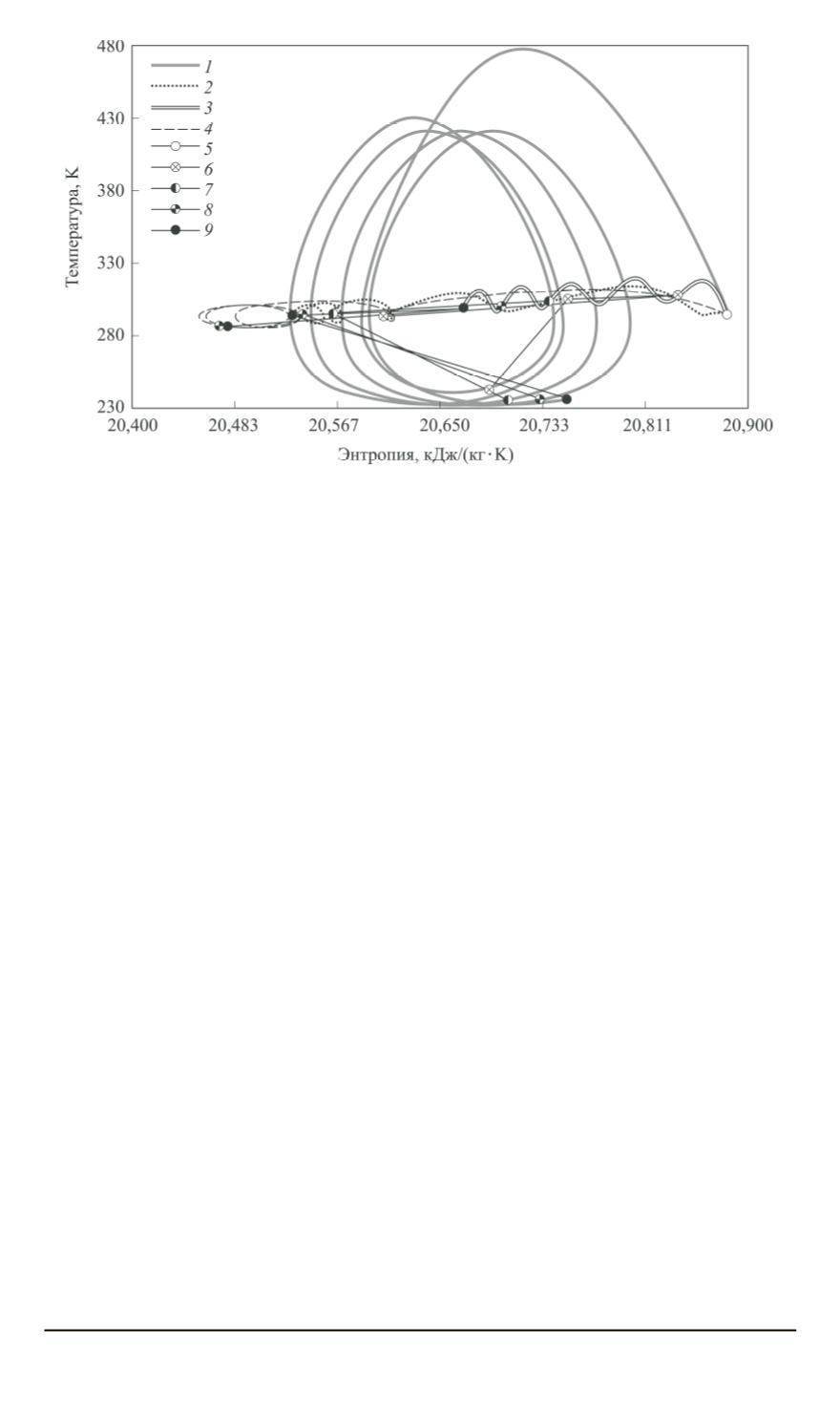
Рис. 6. Процессы для каждой полости КГМ за пять оборотов на диаграмме
T
−
S
Выводы.
1. B ходе работы над расчетной моделью удалось по-
лучить связь между геометрическими параметрами КГМ и временем
выхода на заданный температурный уровень 77 K.
2. Расчетная модель не учитывает осевую теплопроводность реге-
нератора и нуждается в дополнении и корректировке.
ЛИТЕРАТУРА
1.
Оносовский В.В.
Моделирование и оптимизация холодильных установок. Л.:
Изд-во Ленинградского университета, 1990. 208 с.
2.
Самарский А.А.
,
Михайлов А.П.
Математическое моделирование: Идеи. Методы.
Примеры. М.: Физматлит, 2001. 320 с.
3.
Тарасик В.П.
Математическое моделирование технических систем. Мн.:
Дизайн-ПРО, 1997. 641 с.
4.
Архаров А.М.
,
Марфенина И.В.
,
Микулин Е.И.
Криогенные системы. В 2 т. Т. 1.
Основы теории и расчета. М.: Машиностроение, 1966. 576 с.
5.
Архаров А.М.
,
Архаров И.А.
,
Смородин А.И.
Криогенные системы. В 2 т. Т. 2.
Основы проектирования аппаратов, установок и систем. М.: Машиностроение,
1999. 720 с.
6.
Термодинамические
свойства гелия / В.В. Сычев, А.А. Вассерман, А.Д. Козлов
и др. М.: Изд-во стандартов, 1984. 320 с.
REFERENCES
[1] Onosovskiy V.V. Modelirovanie i optimizatsiya kholodil’nykh ustanovok [Modeling
and optimization of refrigeration systems]. Leningrad, Leningradskiy universitet
Publ., 1990. 208 p.
[2] Samarskiy A.A., Mikhaylov A.P. Matematicheskoe modelirovanie: Idei. Metody.
Primery [Mathematical simulation: Ideas. Methods. Examples]. Moscow, Fizmatlit
Publ., 2001. 320 p.
[3] Tarasik V.P. Matematicheskoe modelirovanie tekhnicheskikh sistem [Mathematical
simulation of technical systems]. Minsk, Dizayn-PRO Publ. 1997. 640 p.
114 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2014. № 6


