Analysis of gas-dynamic processes and development of model of flows in hypersonic shock tube

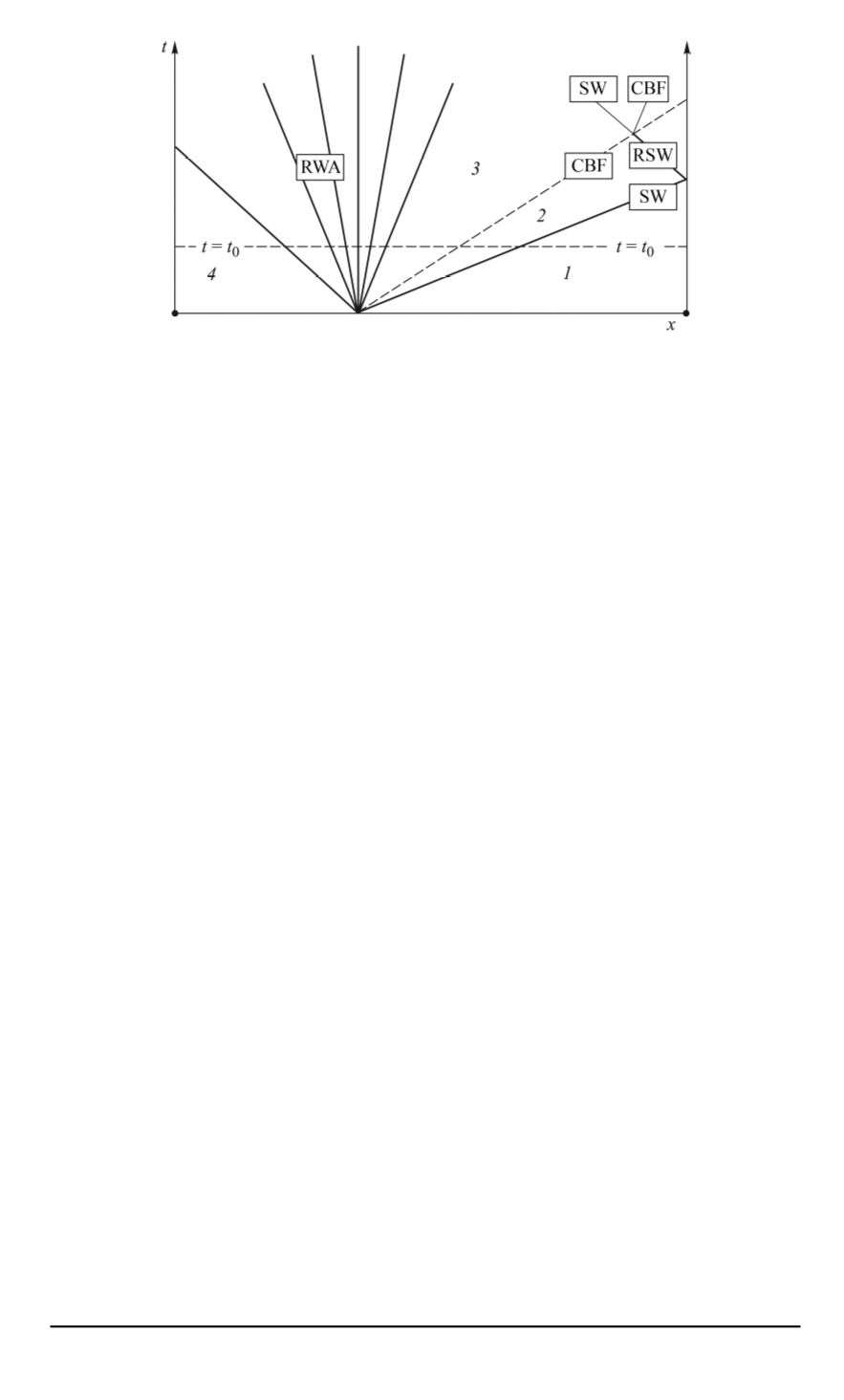
Fig. 1. Diagram of interaction processes of shock waves, rarefaction waves and

contact discontinuities in the one-diaphragm shock tube after the rupture of the

diaphragm:

SW — shock wave front; CBF — contact boundary front; RWA — rarefaction wave area;

RSW — reflected shock wave front

significant (in this case about three times higher) increase of the sound

velocity in the driver gas (

)

and the proportional increase of the ratio

In the shock tubes, the shock wave front surface that is generated in the

test (driven) gas is close to plane and the gas flow in the working path of the

shock tube can be considered one-dimensional in a first approximation. In

the simpliest shock tube, the system of waves mentioned above is generated

after the rupture of the diaphragm (made of metal foil or lavsan film)

separating the low pressure chamber containing the low pressure test gas

(about 0.1. . .0.01 atm), from the high pressure chamber containing the

compressed gas (with pressure from several to hundreds atmospheres).

One of the important tasks in the theory of the shock tube is to establish

mathematical relationships between physical values, which define the state

of gas in a shock tube at the initial time, and the parameters of the system

of mentioned waves at any optional time.

These relationships can be found using methods of mathematical

modeling, which (in case of using high-accuracy computational methods)

reveal the detailed structure of the gas flow that undergoes physical-

chemical transformations, if strong and weak interacting discontinuities

are present in the flow area.

However, despite the development of multidimensional computational

techniques, one-dimensional mathematical models retain their practical

value, in particular, they allow verifying the models describing non-

equilibrium chemical transformations by the comparison of numerical and

experimental results.

The one-dimensional mathematical model of a gas flow in the path of

the shock tube can be developed if a number of simplifying assumptions is

4 ISSN 0236-3941. HERALD of the BMSTU. Series “Mechanical Engineering”. 2014. No. 1