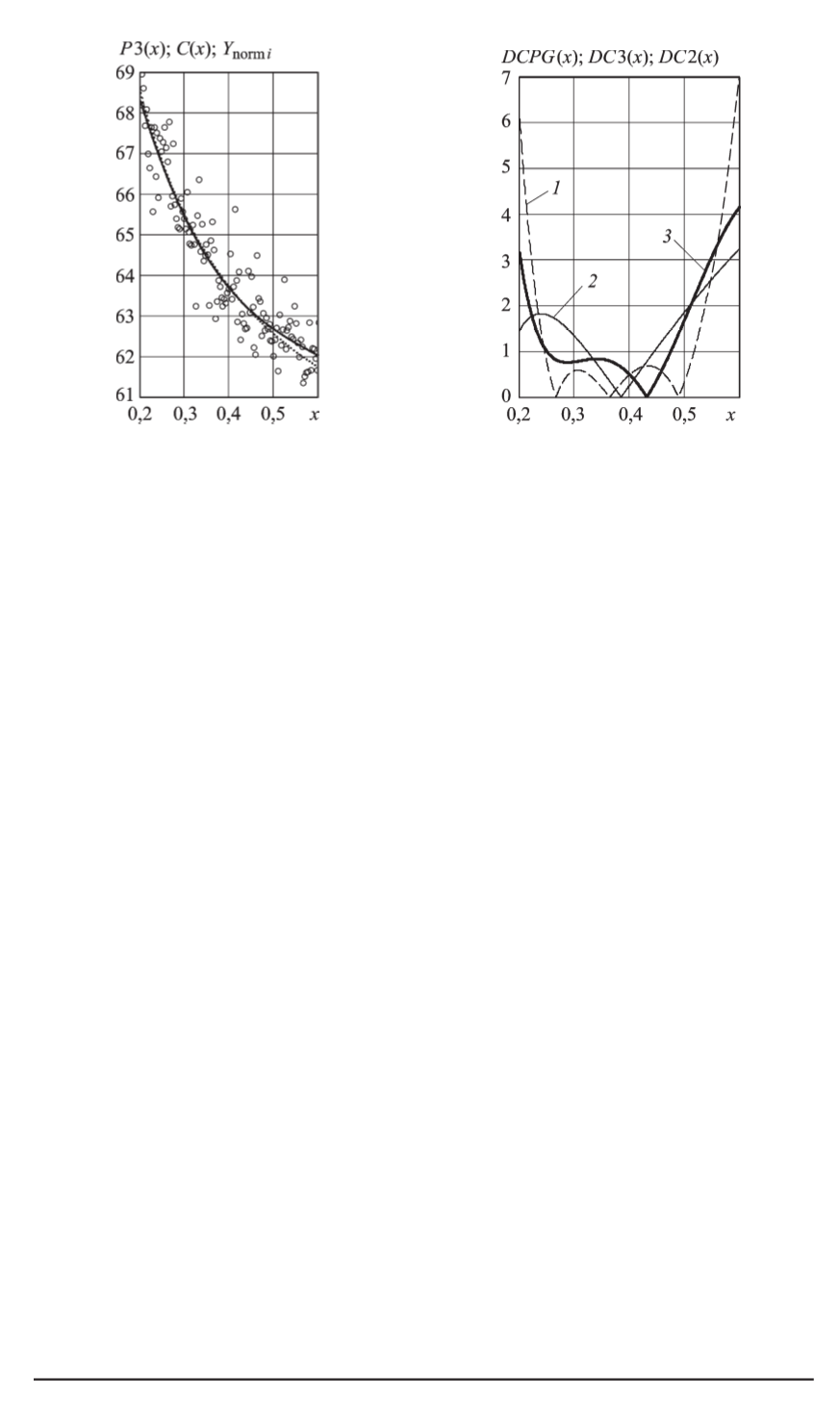
Рис. 1. Зависимости СФП параметра
емкостного преобразователя переме-
щений (сплошная линия) при вос-
становлении полиномом третьей сте-
пени
P
3(
x
)
для истинной функции
C
(
x
)
(штриховая) и при представле-
нии по экспериментальным данным
Y
normi
(кружочки)
Рис. 2. Зависимости модулей при-
веденных истинных погрешностей
DCPG
(
x
) при восстановлении ре-
гуляризующей функцией (
1
) и
полиномами второй (
2
) и третьей (
3
)
степени от измеряемой величины
x
На рис. 4 для тех же аппроксимирующих функций приведены за-
висимости невязок от
N
E
. Это единственная информация о степени
приближения восстановленной функции к экспериментальным дан-
ным, которая доступна в физическом эксперименте. Виртуальный экс-
перимент позволил получить оценку в виде истинных погрешностей.
Легко заметить противоречивость представленных на рис. 3 и 4 ре-
зультатов. Минимум невязок обеспечивается при выборе аппроксими-
рующей функции в виде полинома третьей степени. Минимальные
истинные погрешности достигаются при использовании регуляризую-
щей функции.
По невязкам (физический эксперимент) нельзя принимать решение
о выборе аппроксимирующей функции. Если невязки с увеличением
N
E
уменьшаются на порядок и более, то истинные погрешности слабо
связаны с выбором
N
E
.
На рис. 5 показаны зависимости усредненных максимальных зна-
чений погрешностей по диапазону и по числу восстановлений для
регуляризующей функции и для ее первой производной (чувствитель-
ности). Там же указан коридор рассеяния средних значений погреш-
ностей шириной
6
σ
.
Усредненные истинные погрешности чувствительности превыша-
ют в 3–4 раза погрешности восстановления регуляризующей функции.
Для полиномиальных аппроксимирующих функций погрешности чув-
ствительности увеличиваются значительно больше. Погрешности вто-
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2009. № 4 101


