Параметры течения за фронтом газовой детонации в шероховатых трубах - page 8

ввести некоторый линейный масштаб ¯xS ∼ 1/ψ , уравнения (15) можно
записать в виде
∂ ¯ u
∂ (¯x/ ¯ xS )
= − a
¯ xS ¯
I + a
γ − 1
1 − a ¯ u
¯ xS ¯
Q
γb ¯ p + a ¯ u − 1
;
∂ ¯ p
∂ (¯x/ ¯ xS )
= − c
¯ xS ¯
I
1 − a ¯u
+ g
∂ ¯u
∂ (¯x/ ¯ xS )
.
(16)
Из соотношений (16) следует, что асимптотические распределения
безразмерных давления и массовой скорости за фронтом ДВ в выбран-
ном масштабе длины ¯ xS не зависят от коэффициента трения ψ и опре-
деляются в основном лишь показателем адиабаты ПД γ (для “ сильной”
ДВ это утверждение является строгим, так как в этом случае безразмер-
ные комплексы а , b, с , g в уравнениях (16) и функция ¯
Q зависят только
от γ).
Для оценки влияния показателя адиабаты ПД на асимптотические
распределения ¯ p и ¯u за фронтом ДВ уравнения (15) были также проин-
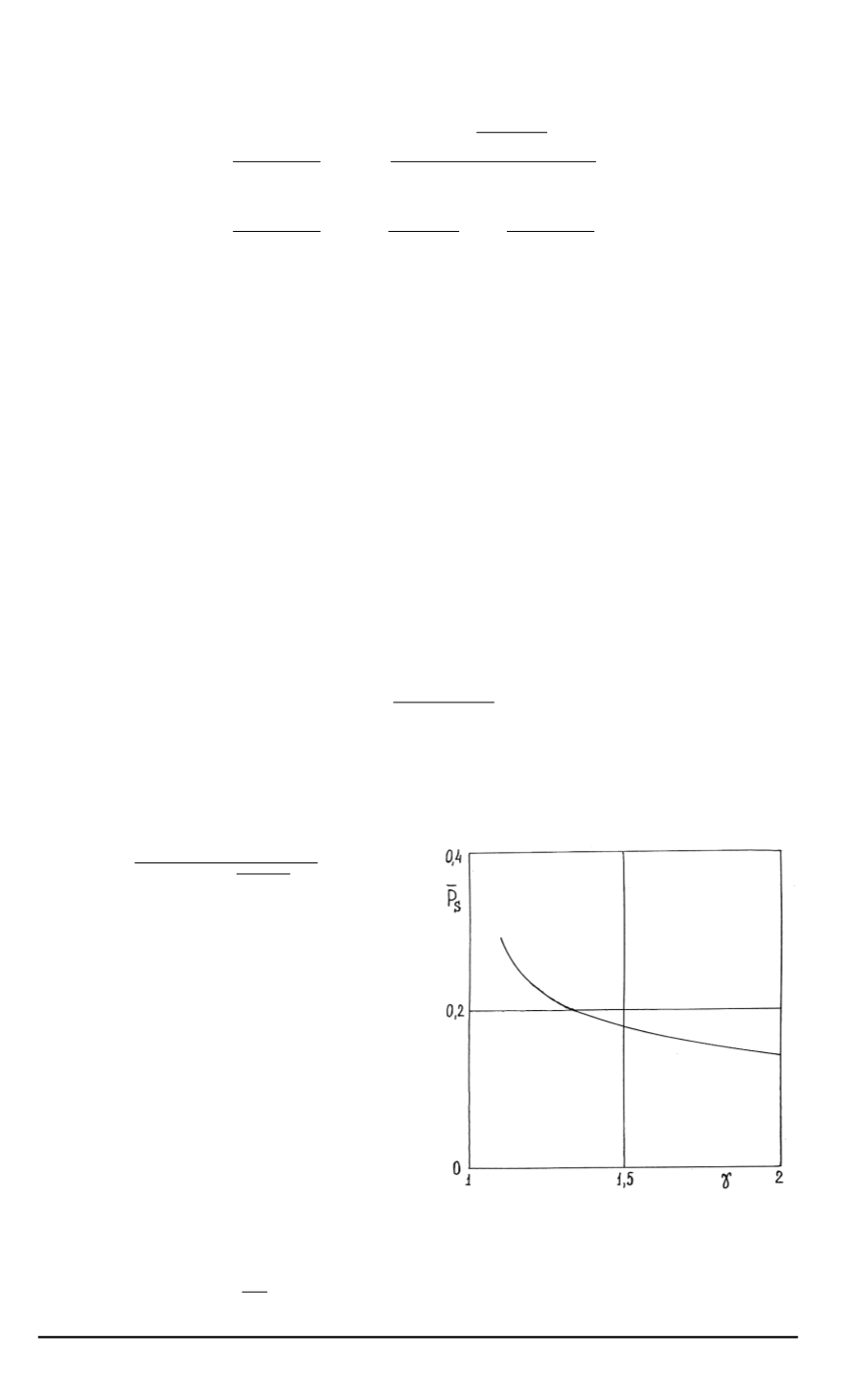
тегрированы для значений γ = 1 ,1; 1,4; 1,7 и 2,0. На рис. 4 приведен
график зависимости величины предельного давления ¯ pS (при ¯x → ∞)
от показателя γ . Эта зависимость хорошо (с погрешностью в пределах
1 %) описывается формулой
¯ pS =
0, 145
( γ − 1) 0,3 . (17)
Асимптотическое распределение массовой скорости в ПД можно
представить в виде функции
Рис. 4. Зависимость величины пре-
дельного давления за фронтом дето-
национной волны от показателя адиа-
баты продуктов детонации
¯ u =
1
³1 + Ap ¯ x/ ¯ xS ´α . (18)
Как отмечалось, линейный мас -
штаб ¯ xS обратно пропорционален
коэффициенту трения ψ, при этом
коэффициент пропорционально-
сти, в принципе, может быть вы -
бран произвольным. Удобно его
принять таким, чтобы при ¯ x = ¯xS
величина ¯ u практически обраща -
лась в ноль. Как показывают расче-
ты, для всех γ значения ¯u становят-
ся меньше 0,01 при
¯ xS =
60
ψ
. (19)
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана . Сер. "Машиностроение". 2004. № 1 39