ноль
,
т
.
е
.
градиенты изменения
u
и
р
при приближении к фронту волны
стремятся к бесконечности
.
Если ввести безразмерные переменные
¯
x
=
x/d
,
¯
p
=
p/p
D
,
¯
u
=
u/u
D
и правые части системы
(9)
¯
I
=
d
u
2
D
I
=
−
ψ
2
¯
u
|
¯
u
|
;
¯
Q
=
d
u
3
D
Q
=
−
ψ
2
|
¯
u
|
·
γ
γ
−
1
p
D
ρ
0
u
2
D
µ
¯
p
(1
−
u
D
D
¯
u
)
−
µ
0
p
0
µp
D
¶
+
¯
u
2
2
¸
,
(
14
)
то уравнения
(13)
принимают вид
∂
¯
u
∂
¯
x
=
−
a
¯
I
+
a
γ
−
1
1
−
a
¯
u
¯
Q
γb
¯
p
+
a
¯
u
−
1
;
∂
¯
p
∂
¯
x
=
−
c
¯
I
1
−
a
¯
u
+
g
∂
¯
u
∂
¯
x
,
(
15
)
где через
а
,
b
,
с
,
g
обозначены безразмерные комплексы
a
=
u
D
D
, b
=
p
D
ρ
0
D
2
, c
=
ρ
0
u
2
D
p
D
, g
=
ρ
0
u
D
D
p
D
.
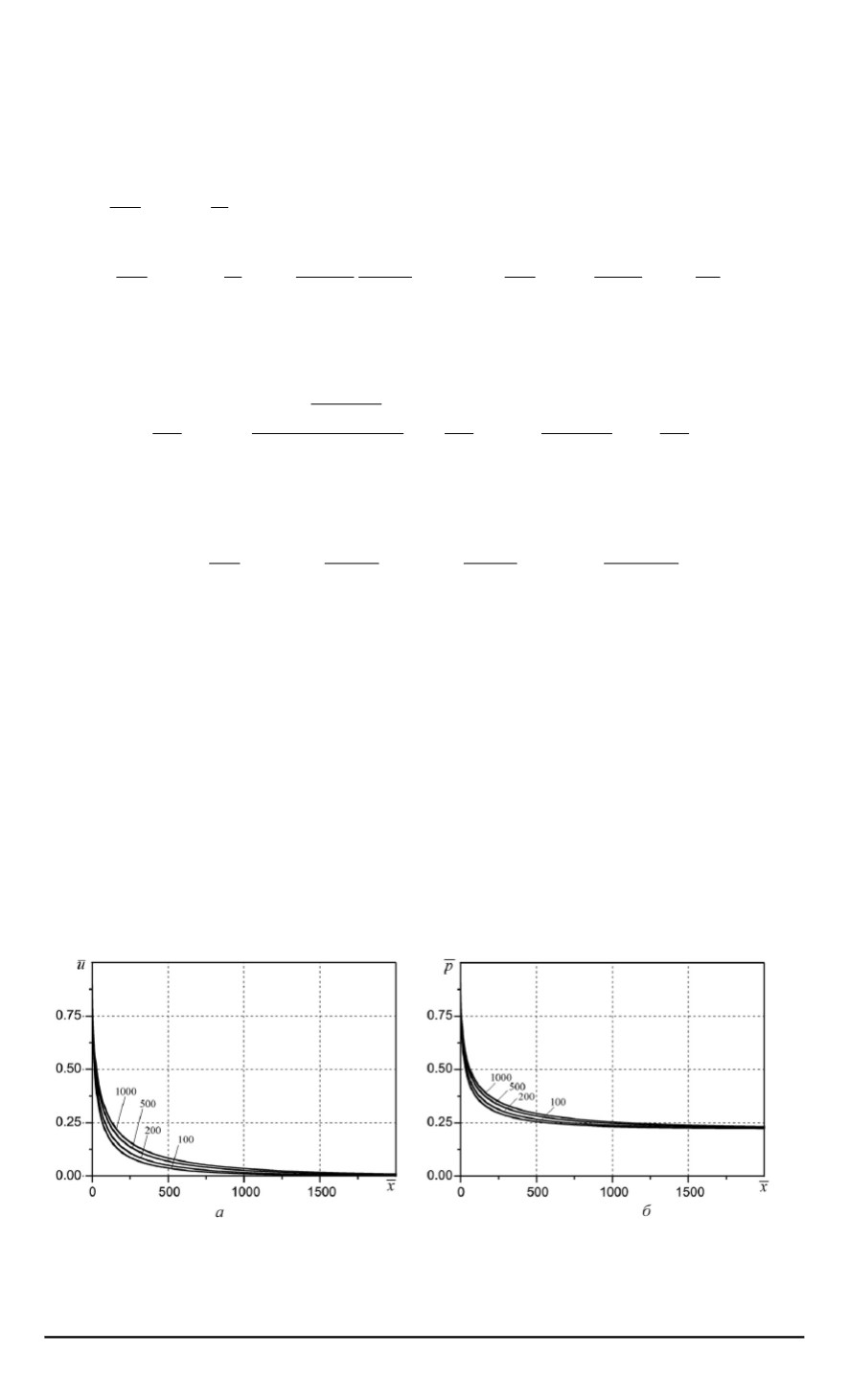
На рис
. 3
приведены асимптотические распределения безразмерных
давления
¯
p
(
а
)
и массовой скорости
¯
u
(
б
)
за фронтом ДВ в трубе с ука
-
занной ранее шероховатостью
(
отмечена числами у кривых
),
получен
-
ные путем интегрирования уравнений
(15).
Видно
,
что с уменьшением
шероховатости
(
ростом отношения
d/ε
)
снижается интенсивность спа
-
да параметров за фронтом ДВ
,
однако во всех случаях на большом уда
-
лении от фронта
¯
u
→
0
,
а безразмерное давление стремится к одной и
той же величине
¯
p
→
¯
p
S
≈
0
,
223
.
Из соотношений
(14)
видно
,
что безразмерные правые части систе
-
мы
(9)
¯
I
и
¯
Q
пропорциональны коэффициенту трения
ψ
,
поэтому
,
если
Рис
. 3.
Асимптотические распределения давления
(
а
)
и массовой скорости
(
б
)
за
фронтом детонационной волны в трубе с различной шероховатостью стенок
;
чи
-
сла у кривых соответствуют значениям отношения
d/ε
38 ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Машиностроение
". 2004.
№
1


