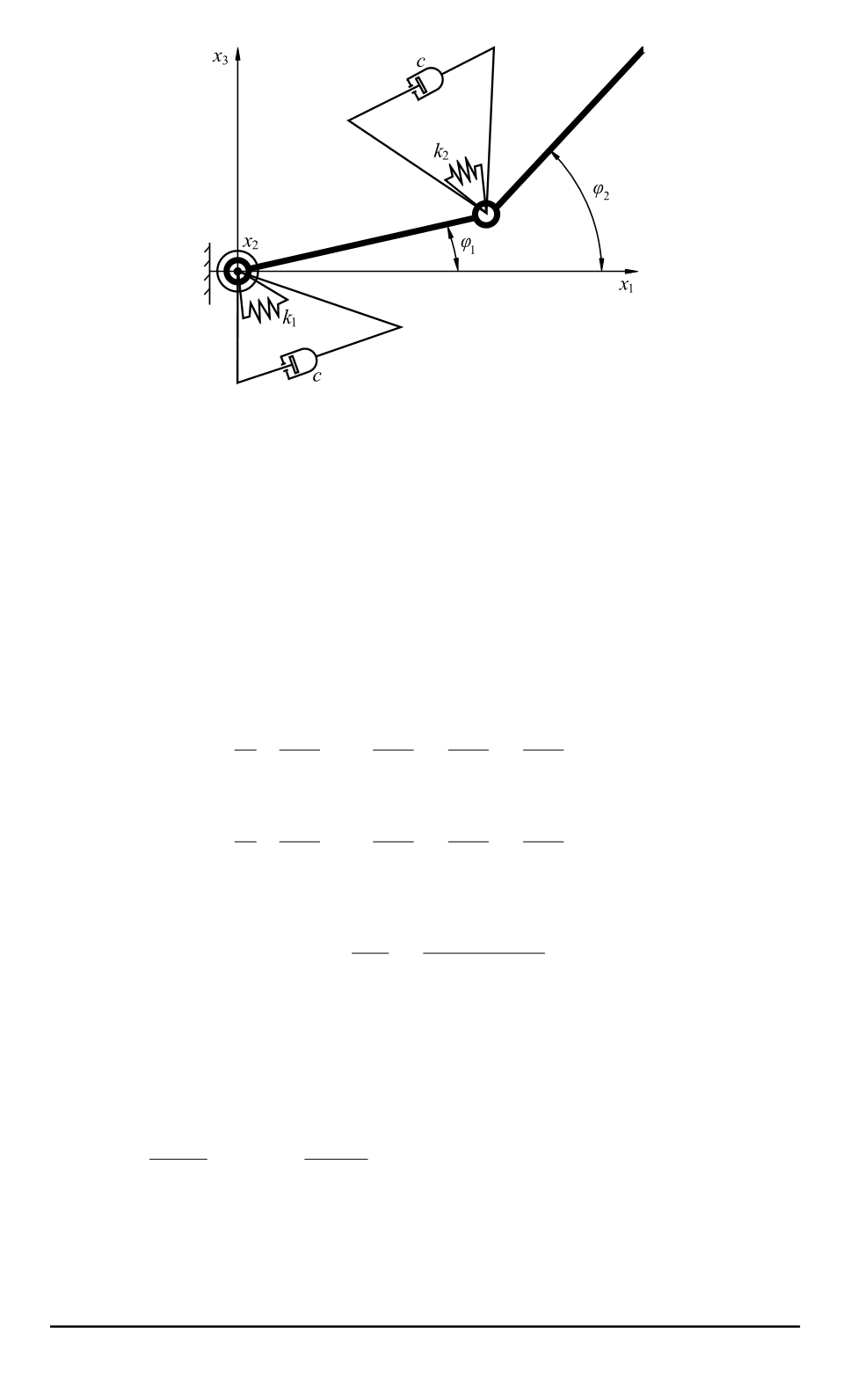
Рис. 4. Двухзвенная модель консольной лопасти
оси
OY
и
OX
— соответственно по бинормали к орбите и по ее
трансверсали в сторону движения центра масс КА. На рис. 3 ось
OY
направлена из плоскости чертежа. Система
Ox
1
x
2
x
3
— средняя систе-
ма координат, она связана с упругим телом (см. рис. 2). На рис. 2 и 3
ось
Ox
2
направлена из плоскости чертежа.
Рассмотрим кососимметричные формы колебаний паруса. Двух-
звенная модель одной лопасти представлена на рис. 4. Уравнения дви-
жения для двухзвенной модели, приведенной на рис. 2 и 4, являются
уравнениями Лагранжа:
d
dt
∂T
∂
˙
ϕ
1
−
∂T
∂ϕ
1
+
∂P
∂ϕ
1
+
∂D
∂
˙
ϕ
1
= 0;
d
dt
∂T
∂
˙
ϕ
2
−
∂T
∂ϕ
2
+
∂P
∂ϕ
2
+
∂D
∂
˙
ϕ
2
= 0
,
(1)
где
D
— диссипативная функция, записываемая в виде
D
=
c
˙
ϕ
2
1
2
+
c
( ˙
ϕ
2
−
˙
ϕ
1
)
2
2
.
(2)
Кинетическая энергия упругого тела в соответствии с методикой,
изложенной в работе [1], входящая в уравнение Лагранжа для двух-
звенника, определяется из уравнения
T
=
T
1
+
T
2
+
T
3
,
(3)
где
T
1
=
m
l
V
2
0
2
;
T
2
=
ω
∙
Iω
2
.
Тензор инерции лопасти паруса
I
=
I
x
1
−
I
x
1
x
2
−
I
x
1
x
3
−
I
x
1
x
2
I
x
2
−
I
x
2
x
3
−
I
x
1
x
3
−
I
x
2
x
3
I
x
3
;
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2006. № 1 17


