
С.В. Федоров, Н.А. Федорова
50
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2016. № 4
растает при
Z
0,1 примерно на 45 % для малопрочной грунтовой преграды
(ГСП1) и на 50 % для высокопрочной горной породы (ГСП3), при
Z
0,25 —
в 2 раза для ГСП1 и в 2,2 раза для ГСП3, при
Z
0,5 — в 2,6 раза для ГСП1 и
в 3 раза для ГСП3 (см. рис. 4). Очевидно, за счет дальнейшего увеличения зна-
чения
Z
(т.
е. увеличения массы ракетного топлива по отношению к массе
ударника) можно получить еще большее увеличение глубины проникания. Од-
нако эта возможность ограничивается чрезвычайно большими перегрузками,
которые испытывает проникающий модуль при движении в преграде. Чтобы
выдержать действие таких перегрузок, проникающий модуль должен иметь вы-
сокопрочную конструкцию с достаточно толстыми стенками корпуса, что ведет
к возрастанию его массы. Поэтому с учетом условия обеспечения необходимой
прочности реализовать на практике конструкцию реактивного проникающего
модуля со значениями числа Циолковского, превышающими несколько десятых
долей единицы, представляется сложным.
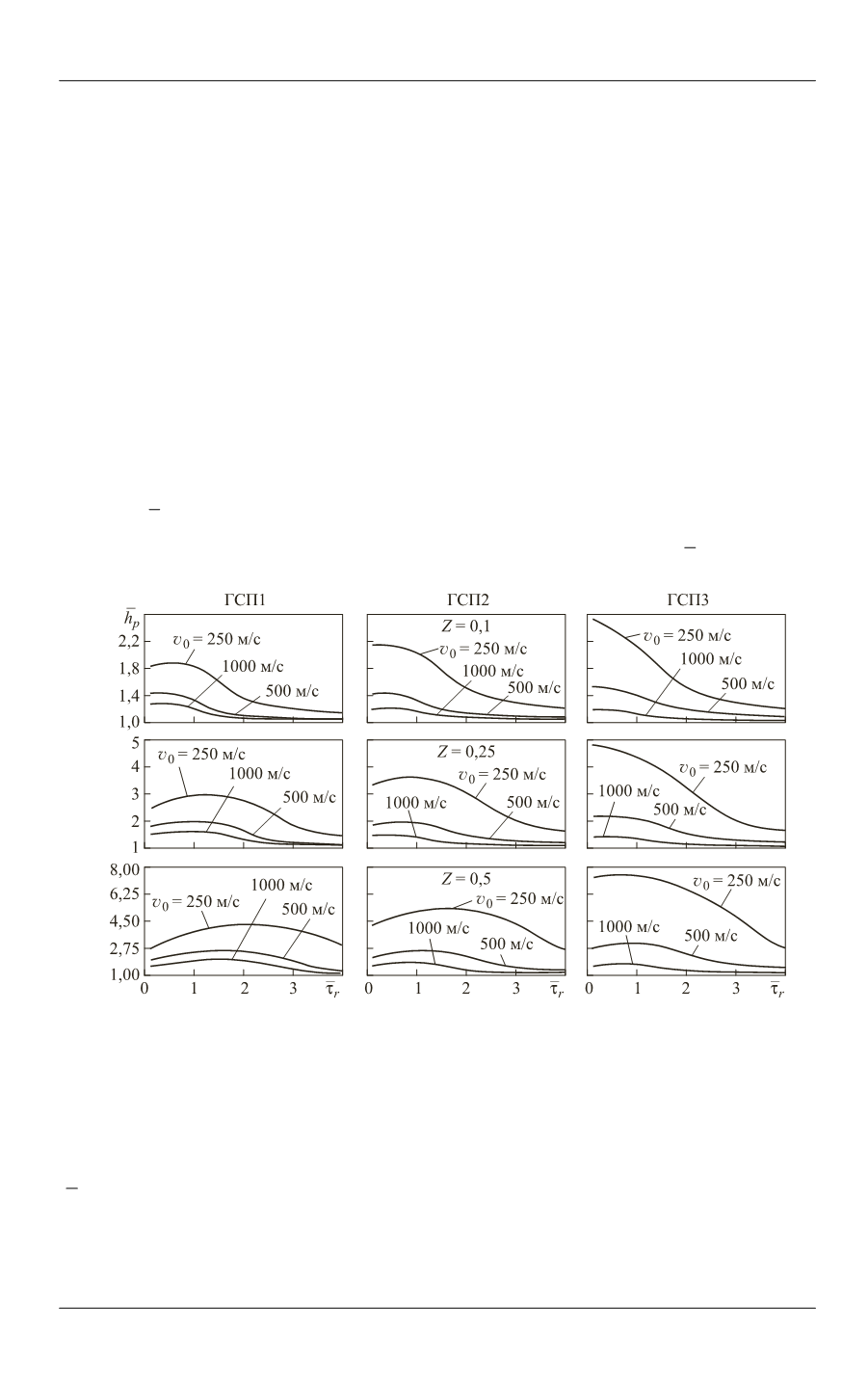
На рис. 6 показано влияние на достигаемый эффект увеличения глубины про-
никания
p
h
начальной скорости реактивного ударника и числа Циолковского при
различных продолжительностях действия реактивного импульса
r
и соответ-
ственно разных соотношениях
r
k
реактивной силы и прочностного сопротивления
преграды. Что касается безразмерного времени включения реактивного двигателя
0
r
t
, то оно составляло от 0 до 0,5 (в зависимости от начальной скорости ударника и
типа грунтово-скальной преграды) и выбиралось из условия достижения макси-
мального увеличения глубины проникания. Как оказалось, с увеличением началь-
Рис. 6.
Влияние начальной скорости реактивного ударника и числа Циолковского на
относительную глубину проникания в грунтово-скальные преграды с различными
прочностными свойствами
















