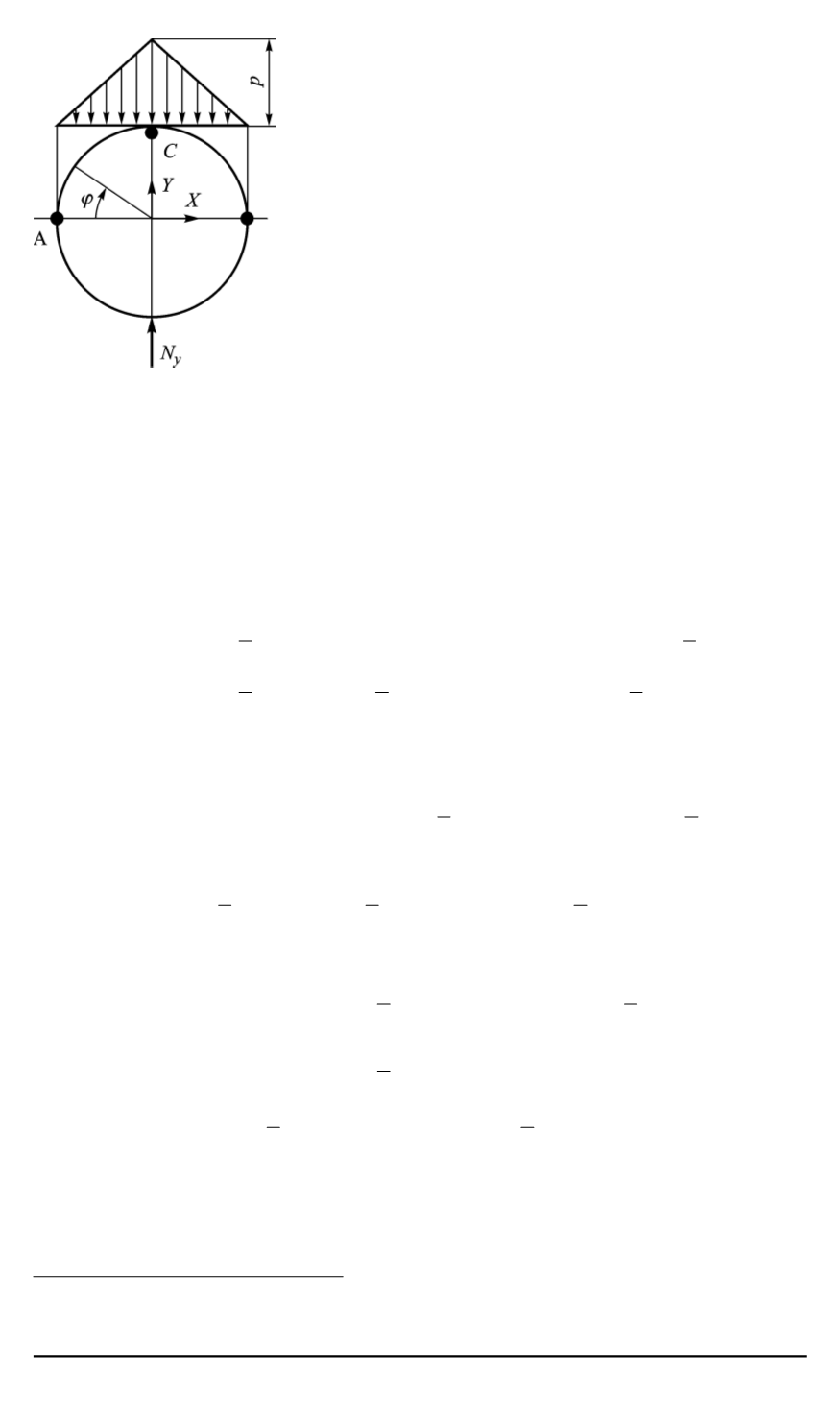
Рис. 1. Аппроксимирую-
щая распределенная на-
грузка на трубу в плоско-
сти
XY
, нормальной оси
Z
трубопровода
внутренними силами (нормальной силой
N
и изгибающим моментом
M
), зависящими от
угла
ϕ
[1] (
ϕ
— угловая координата с отсче-
том от диаметра, ортогонального направлению
действия нагрузки (рис. 1)).
Распределение давлений, действующих на
оболочку радиусом
R
=
D/
2
при учете нерав-
номерности взаимодействия нагрузки в грун-
те с трубой в плоскости
XY
, нормальной оси
трубы, принято в форме треугольника, сим-
метричного относительно оси
Y
(вдоль силы
N
у
=
G
), с максимумом давления
p
=
N
у
/R
.
Предположим, что внешнее давление
p
вызы-
вает только формоизменение оболочки, тогда
гидростатическое давление в жидком продук-
те, заполняющем оболочку на все сечение, не
снижает изгибающих моментов
М
.
При треугольной аппроксимации нагрузки с максимальным давле-
нием
p
нормальная сила
N
в стенке оболочки определяется как
N
=
N
0
cos
ϕ
−
1
2
pR
sin
ϕ
;
N
0
=
−
0
,
02653
pR
0
≤
ϕ
≤
1
2
π
;
N
0
cos
ϕ
−
1
2
pR
sin
ϕ
+
1
2
pR
(1
−
sin
ϕ
)
2
sin
ϕ
1
2
π
≤
ϕ
≤
π
;
(6)
изгибающий момент — по выражениям
M
=
0
,
305
pR
2
−
N
0
R
(1
−
cos
ϕ
)
−
1
2
pR
2
sin
ϕ,
0
≤
ϕ
≤
1
2
π
;
0
,
305
pR
2
−
N
0
R
(1
−
cos
ϕ
)
−
−
1
2
pR
2
sin
ϕ
−
1
6
pR
2
(1
−
sin
ϕ
)
3
1
2
π
≤
ϕ
≤
π ,
(7)
а поперечная сила определяется по уравнениям
Q
=
−
N
0
sin
ϕ
−
1
2
pR
cos
ϕ
0
≤
ϕ
≤
1
2
π
;
−
N
0
sin
ϕ
−
1
2
pR
cos
ϕ
+
+
1
2
pR
(1
−
sin)
2
cos
ϕ
1
2
π
≤
ϕ
≤
π .
(8)
Экстремальные значения усилий в опасных точках
А
(
ϕ
= 0
и
+
π
)
и
С
(
ϕ
=
±
π/
2)
1
можно найти как
N
A
=
−
0
,
02653
pR, N
C
=
−
0
,
5
pR
(9)
1
При аппроксимации распределения нагрузки по закону синуса изгибающий мо-
мент в опасных точках
A
и
C
составляет
M
A
= 0
,
219
P
m
R
2
и
M
C
=
−
0
,
233
P
m
R
2
.
26 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2011. № 4


