течений
,
в их периферийной части максимальные величины составля
-
ющих скоростей соответствуют экспериментальным данным
,
что и по
-
зволяет вычислить интегральные аэродинамические характеристики с
достаточной для инженерной практики точностью
.
В качестве размерных масштабов задачи принимают диаметр дон
-
ного среза
D
,
плотность
ρ
∞
и скорость невозмущенного потока
U
∞
,
скоростной напор
q
=
ρU
∞
2
.
Коэффициент сопротивления
C
x
рас
-
считан для характерной площади поперечного сечения донного среза
S
=
πD
2
/
4
.
Низкорейнольдсовые эффекты на стенке учитываются при
помощи метода пристеночных функций
.
Используется связанная с телом цилиндрическая система коорди
-
нат
x
,
θ
,
y
.
Начало координат расположено в центре цилиндрической
части корпуса
(
т
.
О
),
ось
х
направлена вдоль оси симметрии тела
,
ось
y
расположена в вертикальной плоскости симметрии
.
Внешние границы расчетной области располагаются на значитель
-
ном удалении от омываемых поверхностей тела
(
более
10
калибров ци
-
линдра
).
На входной части границы задаются параметры невозмущен
-
ного потока
,
причем
u
= 1
,
v
= 0
,
p
= 0
.
На выходной части границы
ставятся мягкие граничные условия
(
условия продолжения решения
),
на твердых поверхностях тела
—
условие прилипания
,
на горизонталь
-
ной плоскости симметрии
—
условие непротекания
.
Предполагается
,
что искомое течение имеет плоскость симметрии
y
= 0
,
поэтому реше
-
ние строится в области
y >
0
.
Метод расчета
.
Расчетный алгоритм базируется на процедуре гло
-
бальных итераций для решения конечно
-
объемным методом уравнений
переноса на различных сетках
,
и представляет собой разновидность
SIMPLE-
подобных алгоритмов
(
подробное описание алгоритма мож
-
но найти в работах
[3, 4]).
При конструировании дискретной модели
для аппроксимации конвективных потоков
,
источниковых и нестаци
-
онарных членов уравнений применяется теорема о среднем
,
а для ап
-
проксимации диффузионных потоков
,
с целью предотвратить развитие
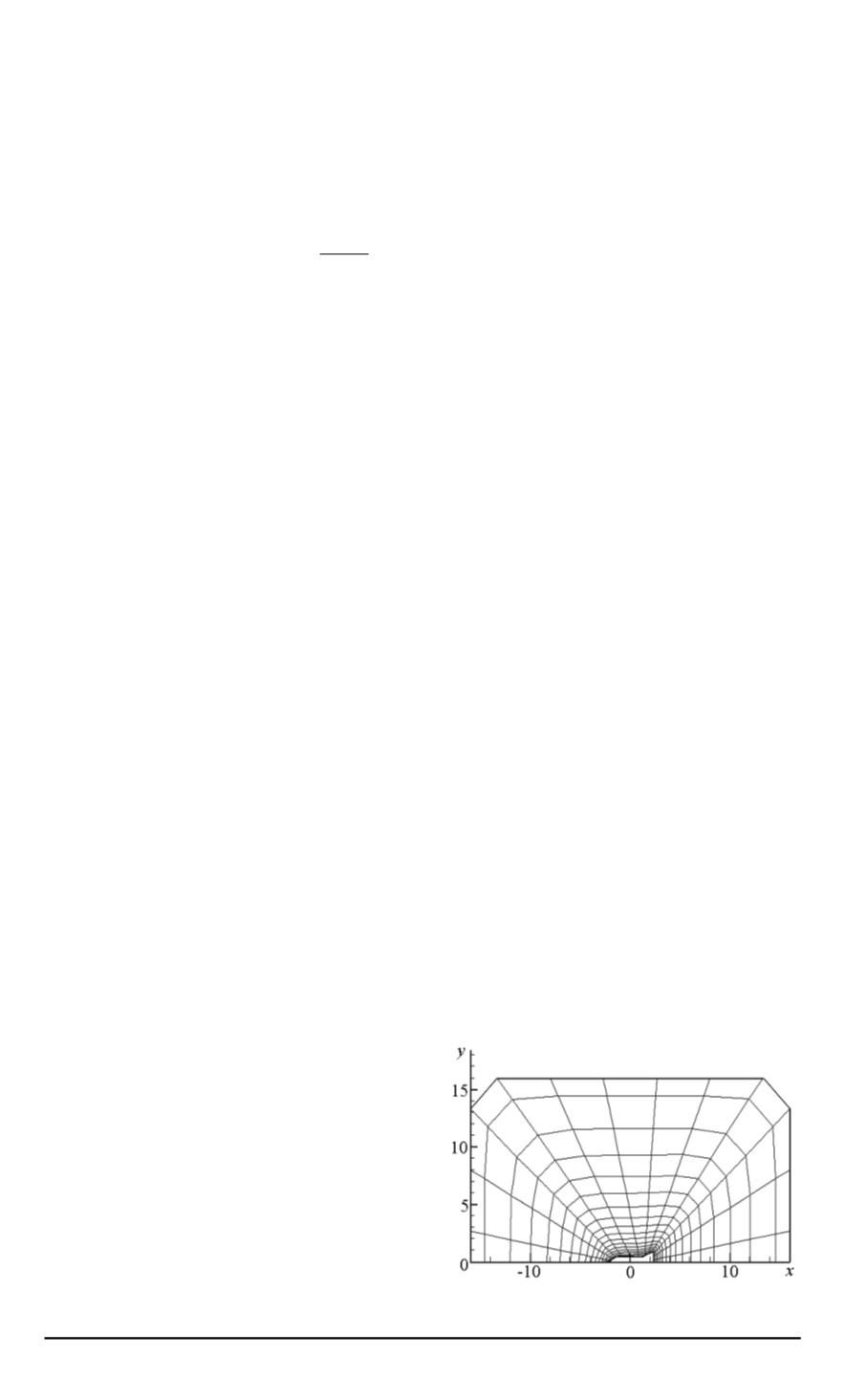
Рис
. 2.
Пример расчетной сетки
шахматного поля решений
,
исполь
-
зуется метод отложенной поправки
.
В рассматриваемой задаче об обте
-
кании осесимметричного тела рас
-
чет проводится на одноблочной не
-
ортогональной структурированной
сетке
,
адаптированной к поверхно
-
сти омываемого тела
.
Узлы расчет
-
ной сетки распределены неравно
-
мерно
(
рис
. 2).
ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Машиностроение
”. 2005.
№
2 23


