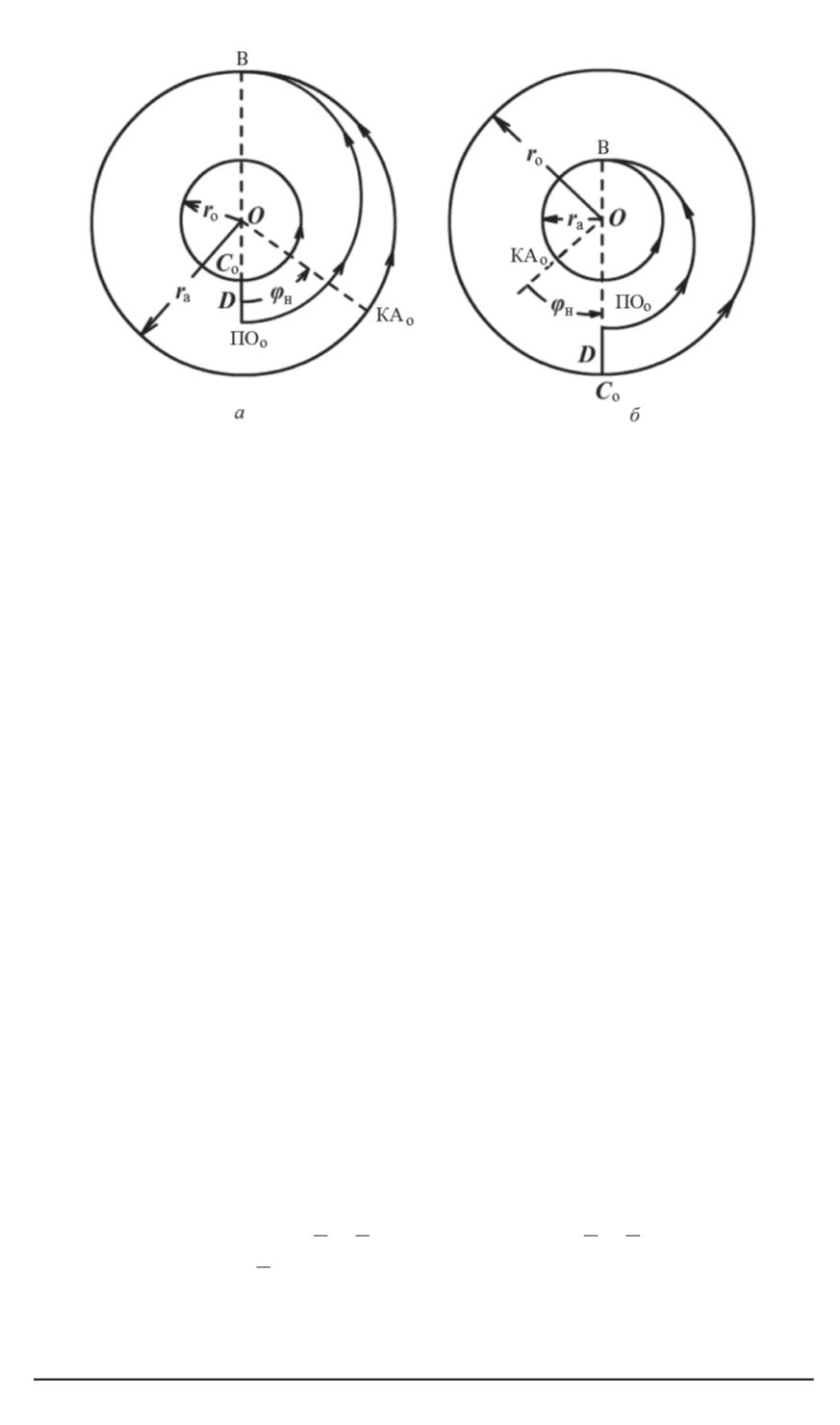
Схемы перехода между орбитами
Известно, что при переходе между круговыми орбитами оптималь-
ным по энергетике является переход по эллипсу, который в апсидаль-
ных точках касается двух рассматриваемых орбит [1]. Поэтому пред-
полагается, что движение ПО от точки расцепления связки (точка ПО,
см. рисунок) до расчетной точки встречи (точка
В
, см. рисунок) про-
исходит по половине эллипса. Угол
ϕ
н
определяет начальное угловое
рассогласование между ПО и КА в момент расцепления связки, при
котором обеспечивается одновременный приход ПО и КА в расчетную
точку встречи.
Одной из основных характеристик ОТС является длина
D
троса,
которая во многом определяет возможности системы для реализации
сближения с КА. Желательно, чтобы целевая задача решалась при ми-
нимальной длине троса. Это позволит уменьшить суммарную массу
тросовой системы и облегчить условия развертывания системы в ра-
бочее состояние. Для сравнительной оценки реализации сближения
ПО и КА из равновесного стационарного режима движения ОТС и из
режимов колебаний и вращения связки вокруг ЦМ воспользуемся за-
висимостями, определяющими требуемую безразмерную длину троса
˜
D
=
D/r
o
.
В случае
r
a
> r
o
+
D
имеем
a
˜
D
4
+
b
˜
D
3
+
c
˜
D
2
+
d
˜
D
+
e
= 0
,
(1)
где
a
= (Ω
ор
+ 1)
2
;
b
=
√
a
[
√
a
(2 + ˜
r
a
) + 2]
;
c
=
√
a
[
√
a
(˜
r
a
+ 1) + 2(2 +
+ ˜
r
a
)] +1
;
d
=
−
[2
√
a
(˜
r
a
+1)+(˜
r
a
+2)]
;
e
= 1
−
˜
r
a
;
Ω
op
— безразмерная
угловая скорость вращения связки относительно орбитальной системы
координат;
˜
r
a
=
r
a
/r
o
.
38 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2009. № 4


