Профилирование лопаточных диффузоров диагональных и радиальных компрессоров - page 4

сохранении углов поворота. Однако это условие неприемлемо для диф -
фузоров центробежных компрессоров, где высота слоя или постоянна
вдоль радиуса, или увеличивается (см. рис. 1). Поэтому условия про -
филирования слоя с f = const не может быть выдержано.
В таком случае необходимо рассмотреть возможность получения
идентичных эпюр скоростей по профилям плоской и пространственной
решеток при заданном законе изменения высоты по радиусу простран-
ственной решетки в результате изменения углов поворота. Известно
[6], что кривым b/t = f (∆α, α2 ) на рис. 2 соответствует вполне опре -
деленное выражение ¯
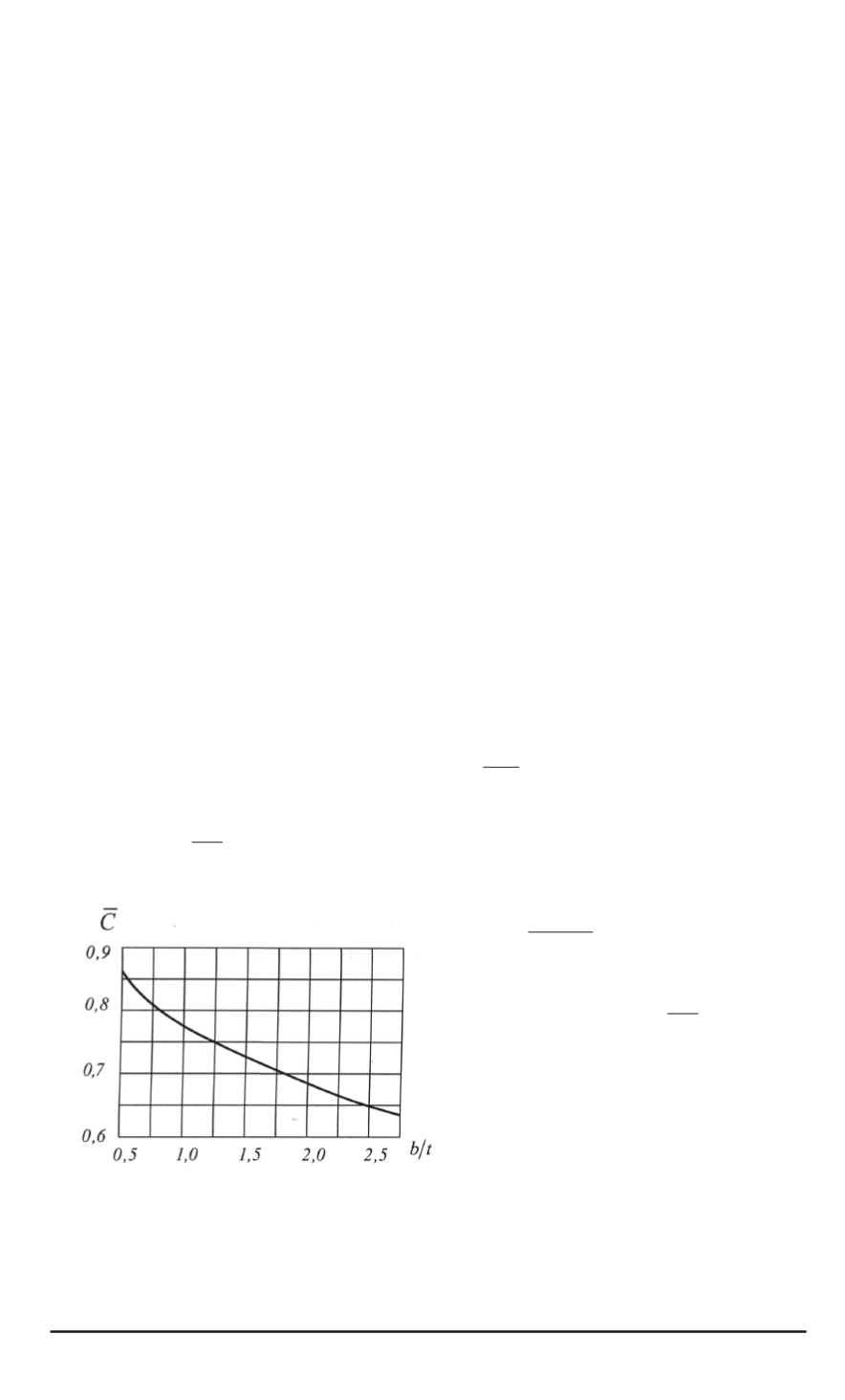
C = C 2/C 1, которое для идеальной несжимаемой
жидкости можно найти из соотношения:
¯
F − 1 = ¯C = sin(α2 − ∆α) / sin(α 2 ),
где C — скорости в решетке, а индексы 1 и 2 относятся ко входу и выхо -
ду решетки соответственно. Зависимость, полученная по данному вы -
ражению из рис. 2, показана на рис. 3, из которого следует, что густоту
решетки можно определять по торможению относительной скорости в
ней.
Введем далее понятие эквивалентной плоской решетки, в которой
густота, степень торможения скорости и , соответственно, геометри -
ческая диффузорность равны. Угол выхода из диагональной решетки
определяется из выражения
sin α 2 = sin α1
¯
F
¯
h ¯
D
.
Здесь ¯
D =
D2
D1
— отношение диаметра выхода к диаметру входа в
Рис. 3. Изменение степени торможения ско-
рости потока от густоты решетки для реше-
ток с номинальным углом поворота
решетку; ¯
h = h2 /h1 = 1 +
+
¯
D − 1
2 ¯h1
tg γm — относи -
тельная высота канала (см.
рис. 1), где ¯
h1 =
h1
D1
. Для пря -
мой эквивалентной решет-
ки sin α 2э = sin α1 ¯
F .
Форма профиля простран-
ственной лопатки определя-
ется конформным преобразо-
ванием из плоской решетки.
В этом случае можно ожи-
дать идентичного распределе-
ния скоростей по лопаткам, а
110 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана . Сер. “Машиностроение”. 2004. № 4