Если истинным является знак
“
<
”,
то считаем
,
что значение
Θ
k
j
+1
явля
-
ется значением параметра
Θ
на данном шаге идентификации
.
Вычислительные аспекты реализации алгоритмов моделиро
-
вания движения и идентификации параметров на базе фильтра
Калмана
.
Численное моделирование процесса оценивания вектора
состояния на базе метода калмановской фильтрации включает в себя
следующие этапы
:
интегрирование нелинейных дифференциальных
уравнений
,
описывающих номинальную
(
или базовую
)
траекторию
;
моделирование измерений путем представления их в качестве функ
-
ций истинного состояния
,
на которые накладываются смещения
(
из
-
за
разности во времени при поступлении сигнала и при его обработке
)
и
шум
;
моделирование реальной траектории
,
заключающееся в приба
-
влении к истинному значению траекторных параметров
,
полученных
при моделировании номинальной
(
базовой траектории
),
случайной
ошибки
.
Тестирование разработанного алгоритма было осуществлено на
примере некоторого гипотетического ЛА со следующими значениями
конструктивных параметров и для следующих начальных параметров
движения
:
V
0
= 3300
м
/
с
;
θ
0
=
−
40
,
13
град
;
h
0
= 30
км
;
m
= 200
кг
;
S
= 0
,
1963
м
2
;
L
= 1
,
176
м
;
I
x
= 3
,
75
кг
·
м
2
;
I
z
= 16
,
95
кг
·
м
2
;
α
0
= 0
,
0
град
.
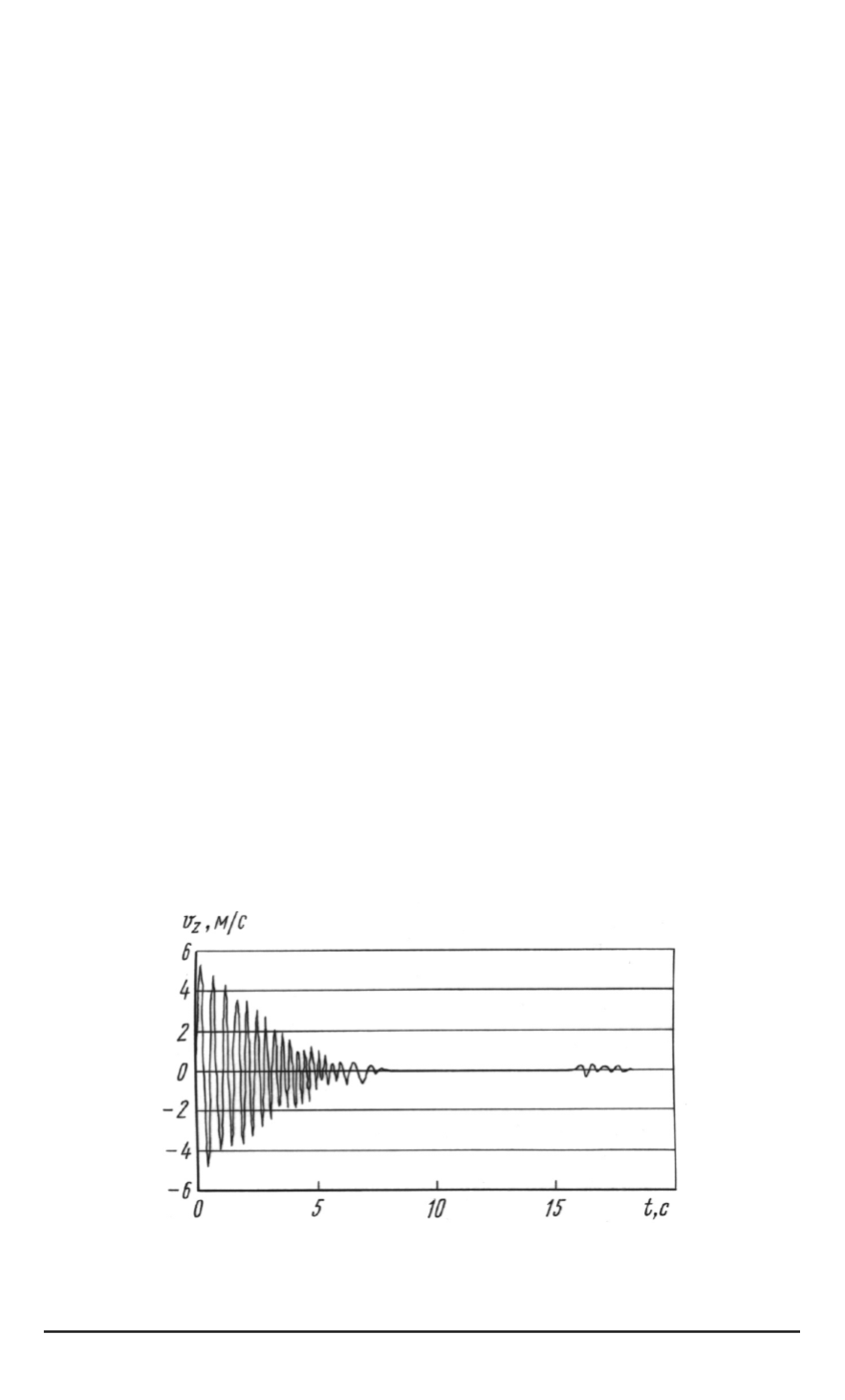
В качестве иллюстрации на рис
. 1
и
2
показаны соответственно кри
-
вые изменения во времени
V
z
и
ω
z
при движении по номинальной тра
-
ектории
,
а на рис
. 3
и
4 —
их значения
,
полученные при использова
-
нии фильтра Калмана
.
Рис
. 5
дает представление об интегральной по
-
грешности моделирования исследуемого процесса на основе сопоста
-
вления результатов численных расчетов по алгоритмам калмановской
Рис
. 1.
Характер изменения составляющей скорости
V
z
в функции времени на
номинальной траектории
ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Машиностроение
”. 2004.
№
4 39


