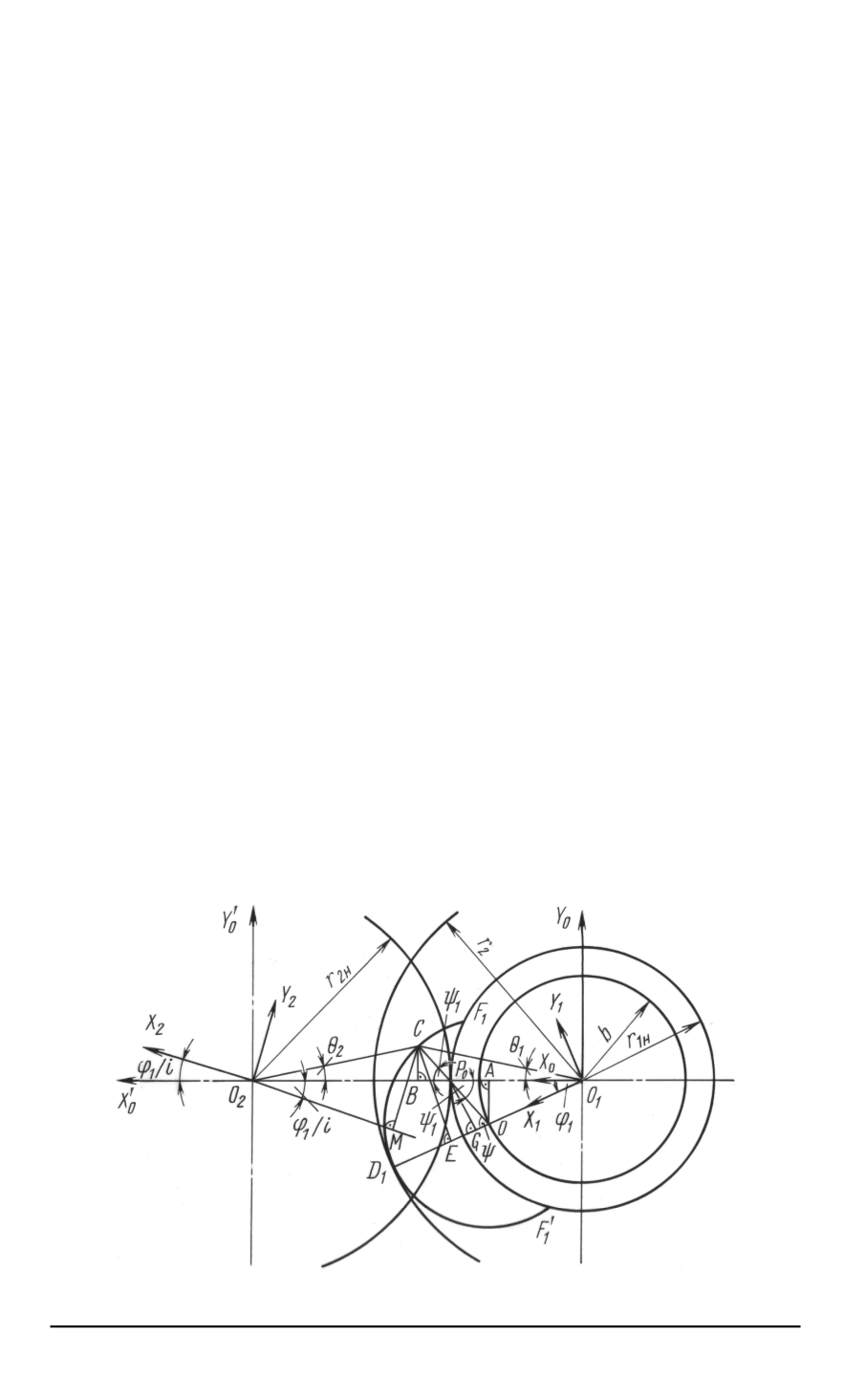
построение профиля зуба, сопряженного с исходным окружным зубом,
графоаналитическим способом.
Для этого выберем четыре системы декартовых координат (рису-
нок):
две подвижные системы координат, из которых —
X
1
O
1
Y
1
жест-
ко связана с исходным ротором, вращается вместе с ним с угловой
скоростью
ω
1
и ее центр
O
1
совпадает с центром исходного ротора;
X
2
O
2
Y
2
жестко связана с сопряженным ротором, вращается вместе
с ним с угловой скоростью
ω
2
и ее центр
O
2
совпадает с центром
сопряженного ротора;
две неподвижные системы координат, из которых —
X
0
O
1
Y
0
связа-
на с исходным ротором и ее центр
O
1
совпадает с центром исходного
ротора;
X
0
0
O
2
Y
0
0
связана с сопряженным ротором и ее центр
O
2
совпа-
дает с центром сопряженного ротора.
Расстояние между центрами координат, межосевое расстояние,
обозначим как
A
.
При построении сопряженного профиля задается исходный про-
филь, т.е. число и профиль зубьев. Примем число зубьев равным
z
1
, а
профиль зуба опишем окружностью радиуса
r
, центр которой лежит
внутри начальной окружности радиуса
r
1н
на расстоянии
b
от центра
O
1
координат
X
1
O
1
Y
1
. Запишем уравнения профиля зуба ведущего
винта в системе координат
X
1
O
1
Y
1
(в параметрической форме):
x
1
=
b
+
r
cos
ψ
;
y
1
=
r
sin
ψ,
)
(1)
где
ψ
— параметр профиля.
Изобразим зуб в произвольном положении, например, при поворо-
те на угол
ϕ
1
координат
X
1
O
1
Y
1
относительно неподвижных коорди-
Построение сопряженного профиля и линии зацепления окружного профиля
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2007. № 3 71


