инерции трубчатого элемента складывающегося стержня относитель-
но основания.
Соотношение (3) можно также получить из равенства потенциаль-
ной и кинетической энергий в момент полного раскрытия:
— потенциальная энергия пружин
Π
0
= 4
N
π
4
(
M
н
+
M
к
) =
πN
(
M
н
+
M
к
)
,
где первый коэффициент равен числу пружин, связанных с одним
складывающимся стержнем;
— кинетическая энергия складывающихся стержней
T
=
1
2
ω
2
k
J
2
N,
где
2
N
— число трубчатых элементов складывающихся стержней.
Из равенства
Π
0
=
T
получаем выражение (3).
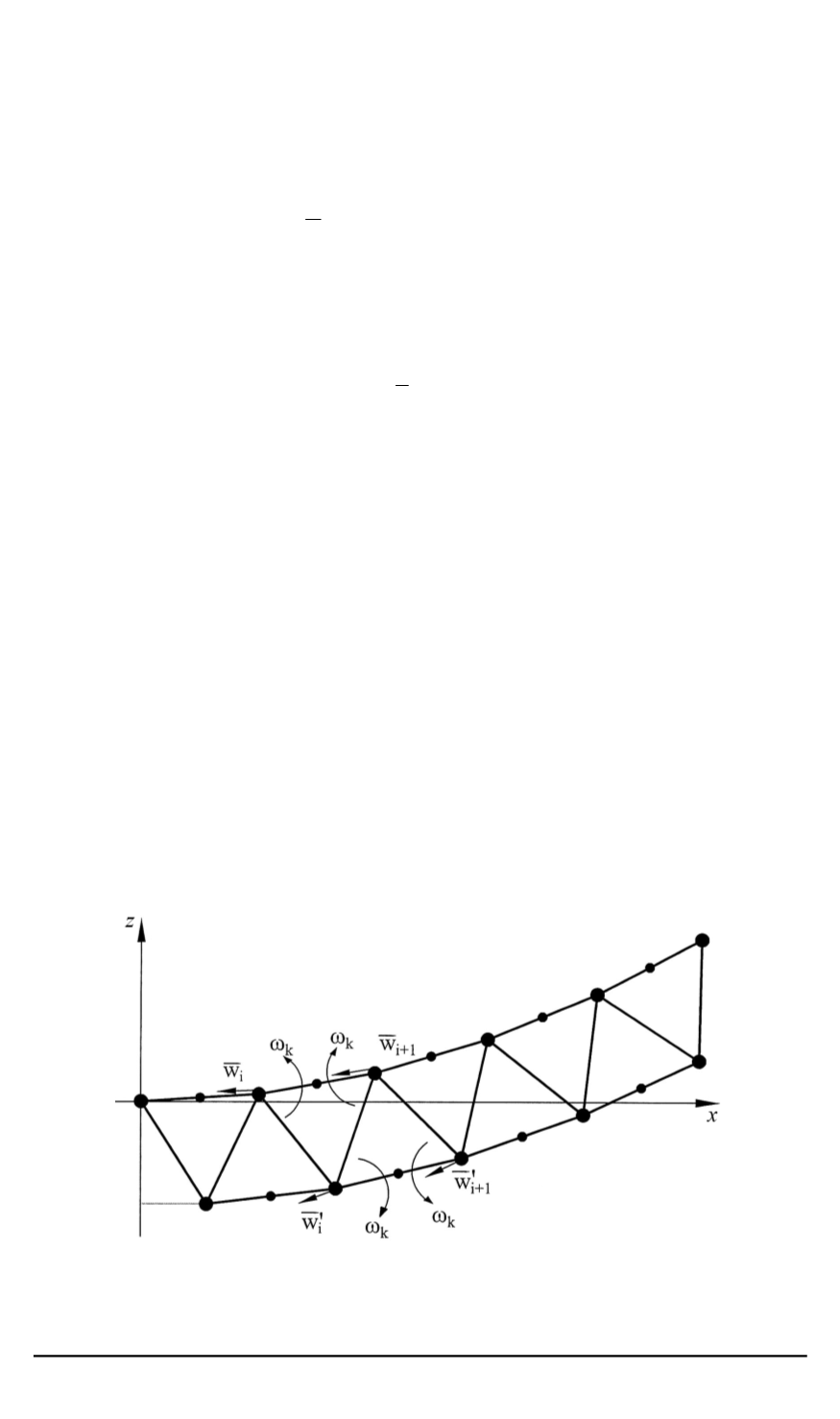
Раскрытому состоянию рефлектора соответствует кинематическая
схема, изображенная на рис. 4. В этом положении линейные скорости
узловых шарниров верхнего и нижнего поясов, а также угловые скоро-
сти вращения диагональных стержней равны нулю, а угловые скорости
вращения складывающихся стержней
ω
k
определяются по зависимо-
сти (3). Кроме того, характерным для этого момента времени является
то, что ускорения узловых шарниров отличны от нуля и направлены к
центру рефлектора. Отличные от нуля указанные кинематические па-
раметры вызывают движение узловых шарниров к центру рефлектора.
Задача определения прочности трубчатых стержневых элементов
при раскрытии ферменных конструкций сводится к исследованию из-
менения во времени напряженно-деформированного состояния упру-
гой конструкции с заданными начальными скоростями (см. рис. 4) и
Рис. 4. Кинематическая схема конструкции:
ω
k
— угловая скорость вращения складывающихся стержней;
ˉ
w
i
,
ˉ
w
0
i
— абсолют-
ные ускорения угловых шарниров верхнего и нижнего поясов конструкции соответ-
ственно
8 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 2


