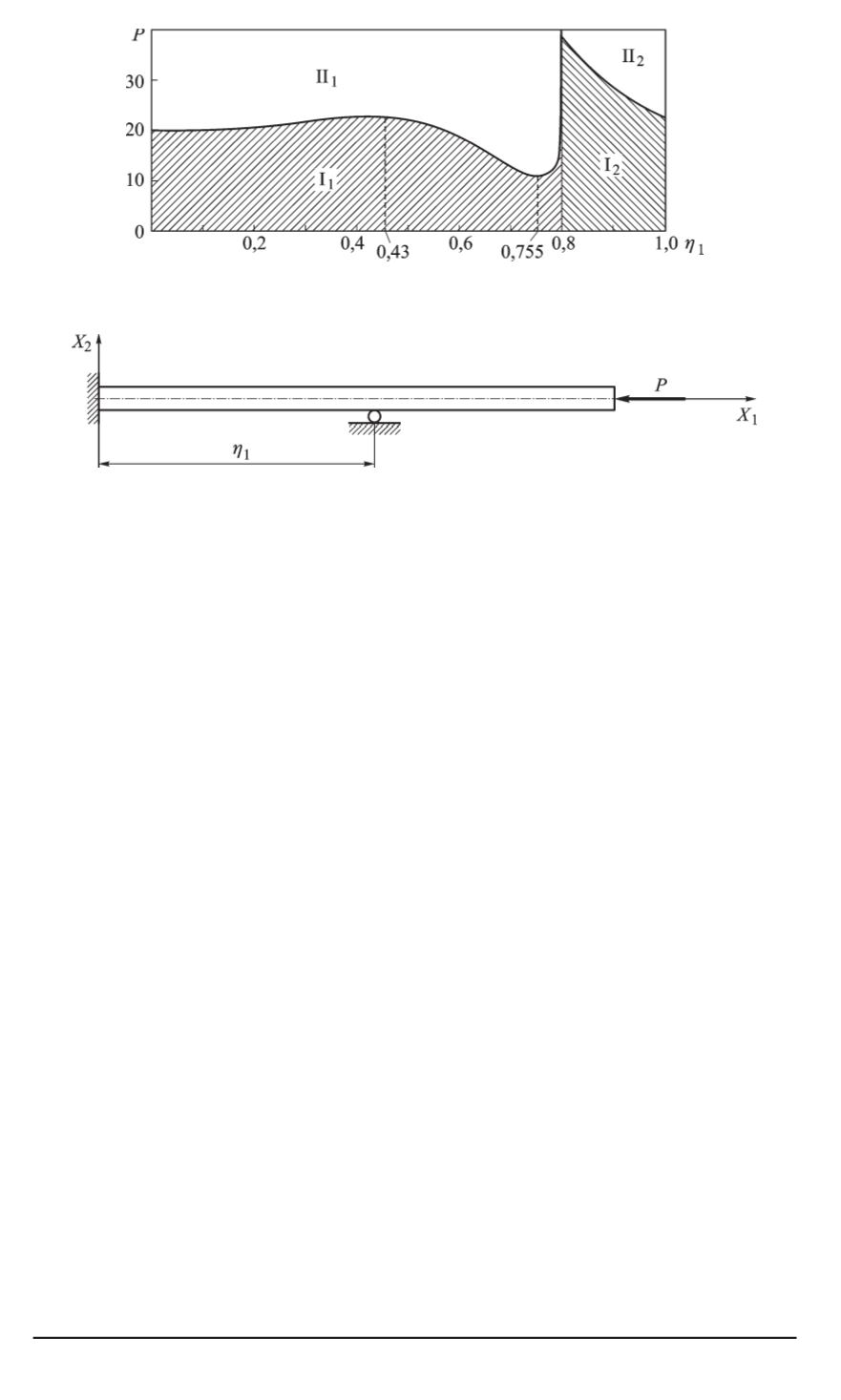
Рис. 3. Области устойчивых (I
1
, I
2
) инеустойчивых (II
1
, II
2
) значений (
P
,
η
1
)
Рис. 4. Стержень с шарнирной локальной связью
На рис. 3 приведен график зависимости
P
∗
от
η
1
, разделяющий на
плоскости
(
P
∗
, η
1
)
устойчивые и неустойчивые области параметров
(
P, η
1
)
. Области I
1
и I
2
— это области параметров
(
P, η
1
)
, при которых
потери устойчивости стержня не происходит; области II
1
и II
2
— это
области параметров, при которых стержень неустойчив. В области
II
1
стержень динамически неустойчив, а в области II
2
— статически
неустойчив. При переходе системы из области II
1
в область II
2
при
η
1
0
,
8
резко возрастает сила
P
, которую может выдержать стержень,
не теряя статической устойчивости. Например, на рис. 3 при
η
1
= 0
,
79
критическая сила
P
∗
= 13
,
47
, а при
η
1
= 0
,
81
—
P
∗
= 39
,
04
, т.е.
значение критической силы увеличивается почти в 3 раза.
В статье [5] приведены результаты численного исследования устой-
чивости стержня, нагруженного следящей силой
P
, для предельного
случая (
c
→ ∞
)
, когда имеется шарнирная локальная связь (рис. 4).
В этом предельном случае при
η
1
<
0
,
5
имеет место динамическая
неустойчивость, а при
η
1
>
0
,
5
— статическая [5].
На рис. 5 приведены графики изменения корней
α
j
и
β
j
в зависи-
мости от
P
при
η
1
= 0
,
51
для:
c
=
∞
(шарнирная опора, рис. 5,
а
);
c
= 150
(рис. 5,
б
) и
c
= 50
(рис. 5,
в
). При
c
=
∞
имеет место стати-
ческая потеря устойчивости, при
c
= 150
и
c
= 50
— динамическая.
Безразмерная жесткость
c
=
c
раз
(
l
3
/A
33
)
.
На рис. 6 представлены графики зависимости комплексных кор-
ней
α
j
и
β
j
от силы притяжения магнита
P
для ряда значений
η
1
,
когда участок стержня находится между магнитами (рис. 7). В этом
случае при отклонении стержня от прямолинейной формы на него в
окрестности точки
K
действует сила притяжения, направление кото-
20 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2010. № 2


