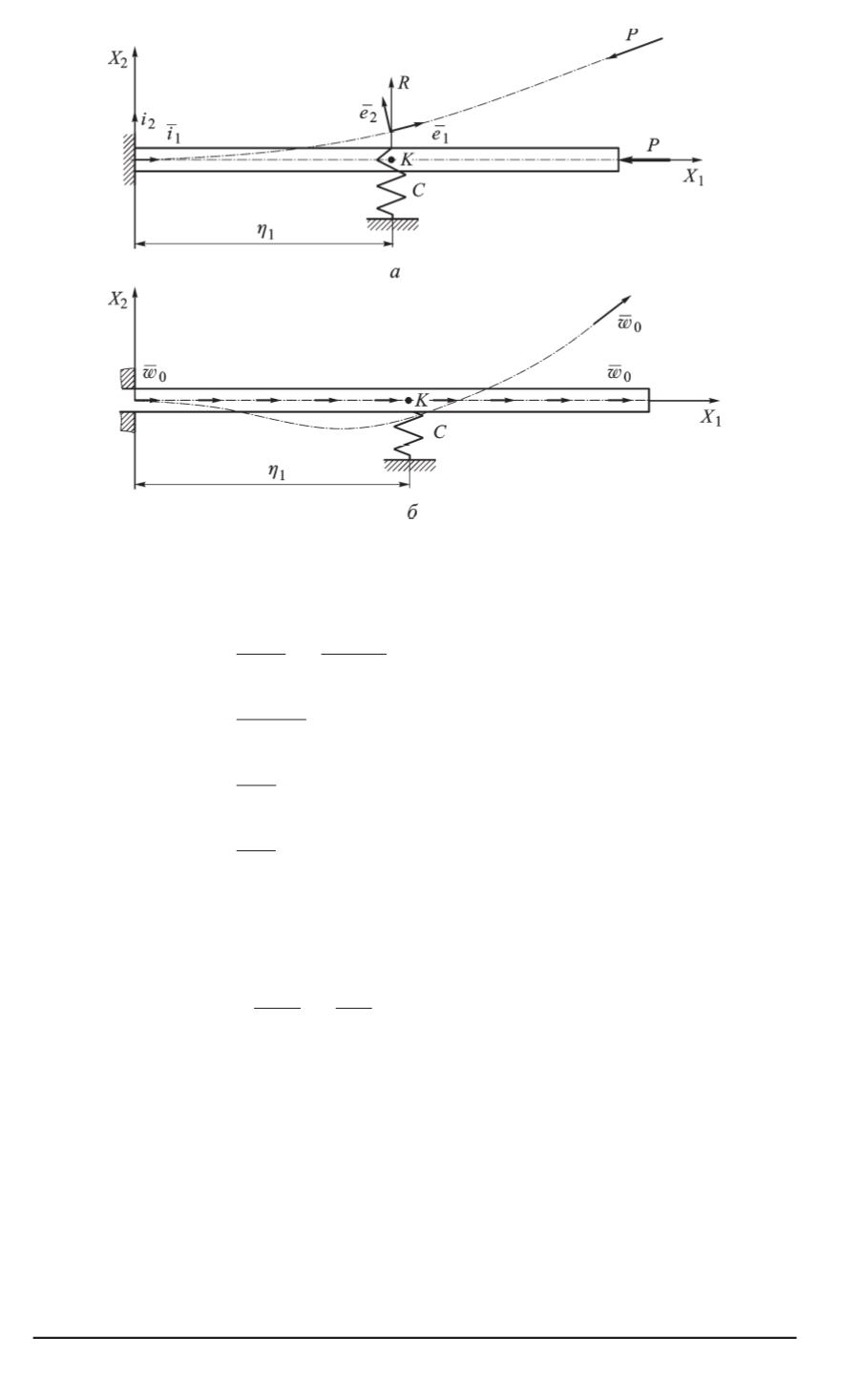
Рис. 1. Прямолинейные стержни с локальной упругой связью
малых колебаний стержня в плоскости
X
1
OX
2
:
∂
2
u
2
∂τ
2
−
∂
Δ
Q
2
∂η
−
Q
10
Δ
M
3
= Δ
q
2
;
∂
Δ
M
3
∂η
+ Δ
Q
2
= 0;
∂ϑ
3
∂η
−
Δ
M
3
= 0;
∂u
2
∂η
−
ϑ
3
= 0
,
(1)
где
Δ
M
3
=
A
33
Δ
k
3
=Δ
k
3
;
Q
10
=
−
P
;
Δ
q
2
=
Rδ
(
η
−
η
1
) =
−
cu
2
δ
(
η
−
η
1
)
.
Систему уравнений (1) можно записать в виде векторного уравне-
ния
A
(1)
∂
2
Z
∂τ
2
+
∂Z
∂η
+
A
(2)
Z
=
bδ
(
η
−
η
1
)
,
(2)
где
Z
= (Δ
Q
2
,
Δ
M
3
, ϑ
3
, u
2
)
т
— вектор состояния;
A
(1)
=
⎡ ⎢⎢⎣
0 0 0
−
1
0 0 0 0
0 0 0 0
0 0 0 0
⎤ ⎥⎥⎦
;
A
(2)
=
⎡ ⎢⎢⎣
0
−
P
0 0
1 0 0 0
0
−
1 0 0
0 0
−
1 0
⎤ ⎥⎥⎦
;
b
= (
cu
2
,
0
,
0
,
0)
т
.
Определение комплексных собственных значений.
Решение уравне-
ния (2) находим в виде
16 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2010. № 2


