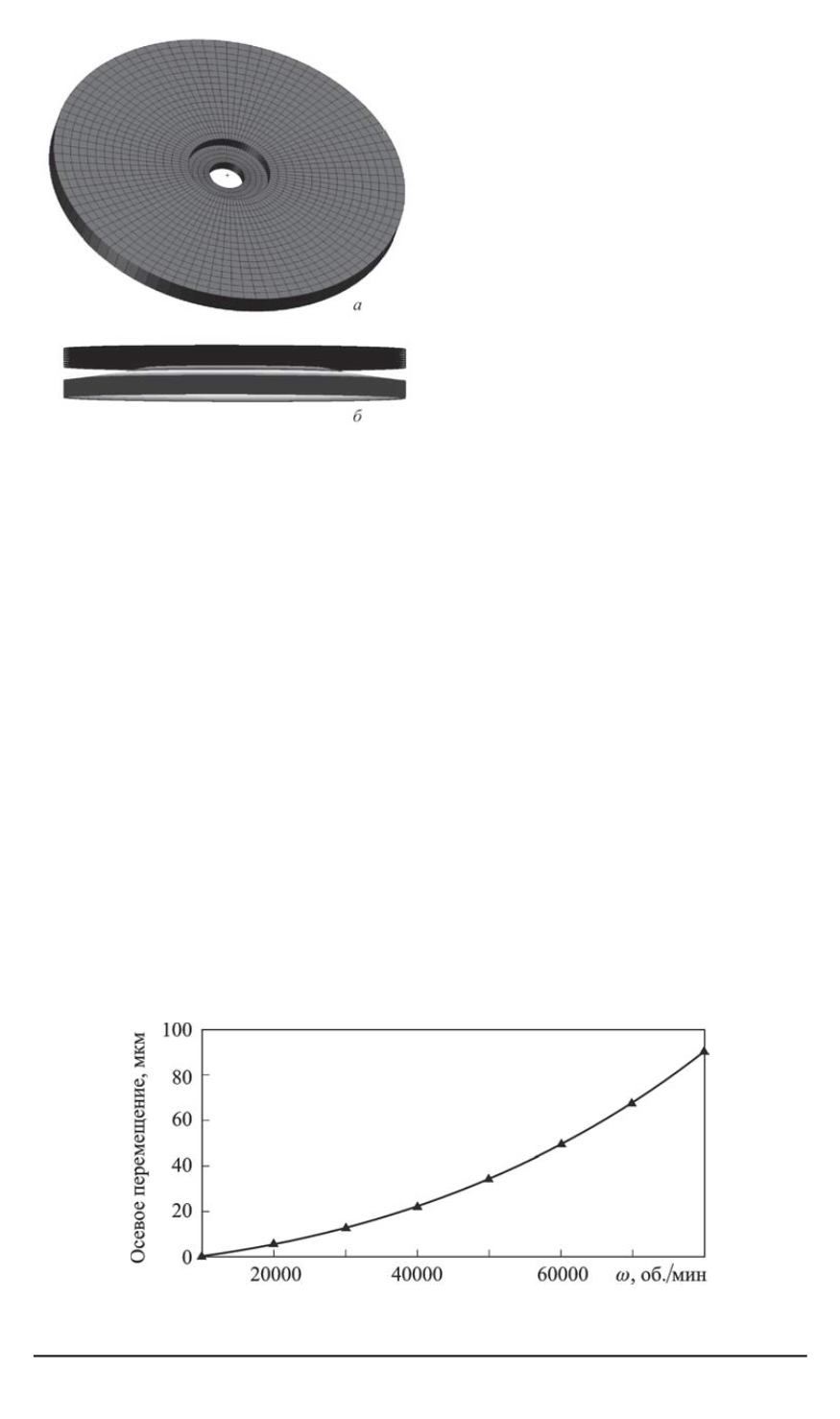
Рис. 6. Точная геометрия модели рабоче-
го диска (
а
) и модель его изгиба (
б
) под
действием центробежных сил при высо-
ких частотах вращения
увеличении частот вращения не-
обходимо обращать особое вни-
мание на уменьшение осево-
го зазора, ведь его уменьшение
до критического значения может
привести к заклиниванию рабо-
чего диска и выход из строя всей
конструкции. Влияние измене-
ния осевого зазора также рас-
пространяется и на откачные ха-
рактеристики насоса в целом.
Быстрота
действия
молекулярно-вязкостного ваку-
умного насоса подвержена изме-
нению под влиянием нескольких
факторов, например, таких как
осевой зазор и частота враще-
ния рабочего диска. Предста-
вленные на рис. 9 расчетные данные получены посредством матема-
тического моделирования процессов, протекающих в рабочем канале
МВВН, с использованием метода Монте-Карло при молекулярном
режиме течения откачиваемого газа [1].
Рост быстроты действия насоса (см. рис. 9) за счет повышения
частоты вращения рабочего диска вполне ожидаем. Изначально пред-
полагалось, что эти две величины связаны в прямой пропорциональ-
ности. Однако при рассмотрении влияния прочих факторов, в част-
ности влияния осевого зазора между рабочим и статорным диском,
прямопропорциональная зависимость не столь очевидна. Как следует
из рис. 9, быстрота действия насоса имеет тенденцию к снижению,
по мере уменьшения осевого зазора, который в свою очередь зависит
от изменения частоты вращения рабочего диска. При рассмотрении
влияния обоих этих факторов, очевидно, что быстрота действия на-
соса ограничивается на том или ином участке диапазона изменения
Рис. 7. Зависимость максимального осевого перемещения при изгибе от частоты
вращения
112 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2010. № 1


