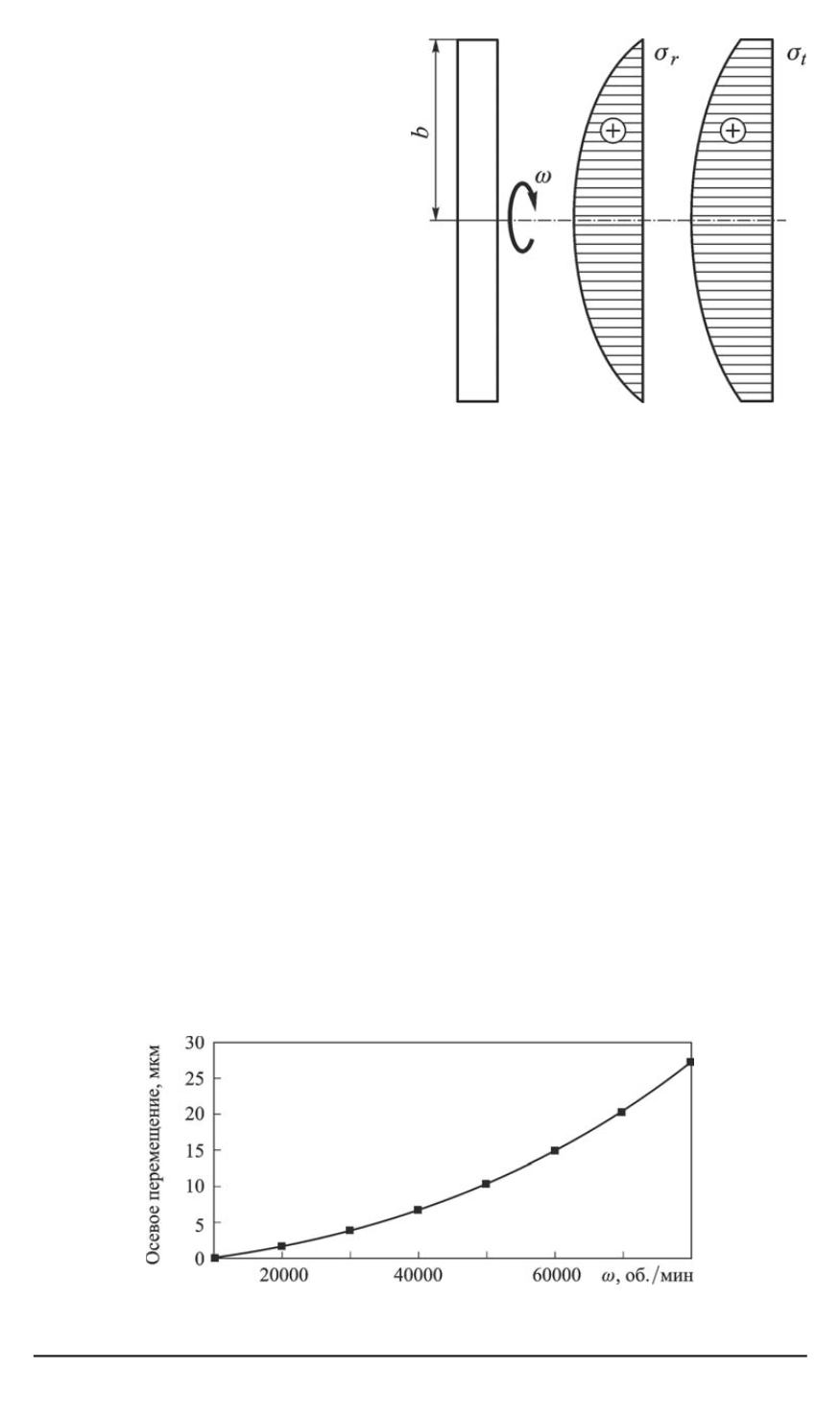
Рис. 4. Эпюры радиального и окружного
напряжения
напряжения примут вид (рис. 4)
[3]
σ
r
=
ρω
2
(3 +
μ
)
b
2
и
(3)
σ
t
=
ρω
2
(3 +
μ
)
b
2
,
где
μ
— коэффициент Пуансона.
Рассчитывается влияние по-
лученных напряжений на осе-
вой зазор между роторным и
статорным дисками. Исходные
данные для расчета: материал
— алюминиевый сплав АК6,
ρ
= 2700
кг/м
3
,
μ
= 0
,
34
,
Е
= 70
ГПа; диск —
b
= 0
,
06
м;
ω
— переменная.
В результате расчетов при условии постоянства объема получена
зависимость максимального осевого перемещения от частоты враще-
ния (рис. 5).
В работе рассматривается влияние центробежных сил на модель
рабочего диска с достаточной степенью приближения (рис. 6). При
помощи компьютерного моделирования получена зависимость макси-
мального осевого перемещения под влиянием центробежных сил на
изгиб рабочего диска при вращении с различными частотами (рис. 7).
Напряжения, возникающие под действием центробежных сил при
вращении, влияют на изменение осевого зазора в противоположных
направлениях. Растягивающие напряжения увеличивают осевой зазор,
а изгибающие — уменьшают его. Для определения итогового осевого
перемещения учитывается влияние обоих явлений (рис. 8).
Как следует из полученных расчетных данных, осевое перемеще-
ние пропорционально частоте вращения рабочего диска. Если на низ-
ких частотах влияние на осевой зазор не столь существенно, то при
Рис. 5. Зависимость максимального осевого перемещения при радиальном удли-
нении от частоты вращения
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2010. № 1 111


