
С.Л. Финогенов, А.И. Коломенцев
70
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2017. № 2
Дифференциальное уравнение (1) в общем случае не имеет аналитического
решения и решается численно (с достаточной точностью) или приближенно с по-
мощью разложения в ряды. В настоящей работе приводятся результаты численно-
го интегрирования методом Рунге —Кутты—Фельберга 4-го и 5-го порядков.
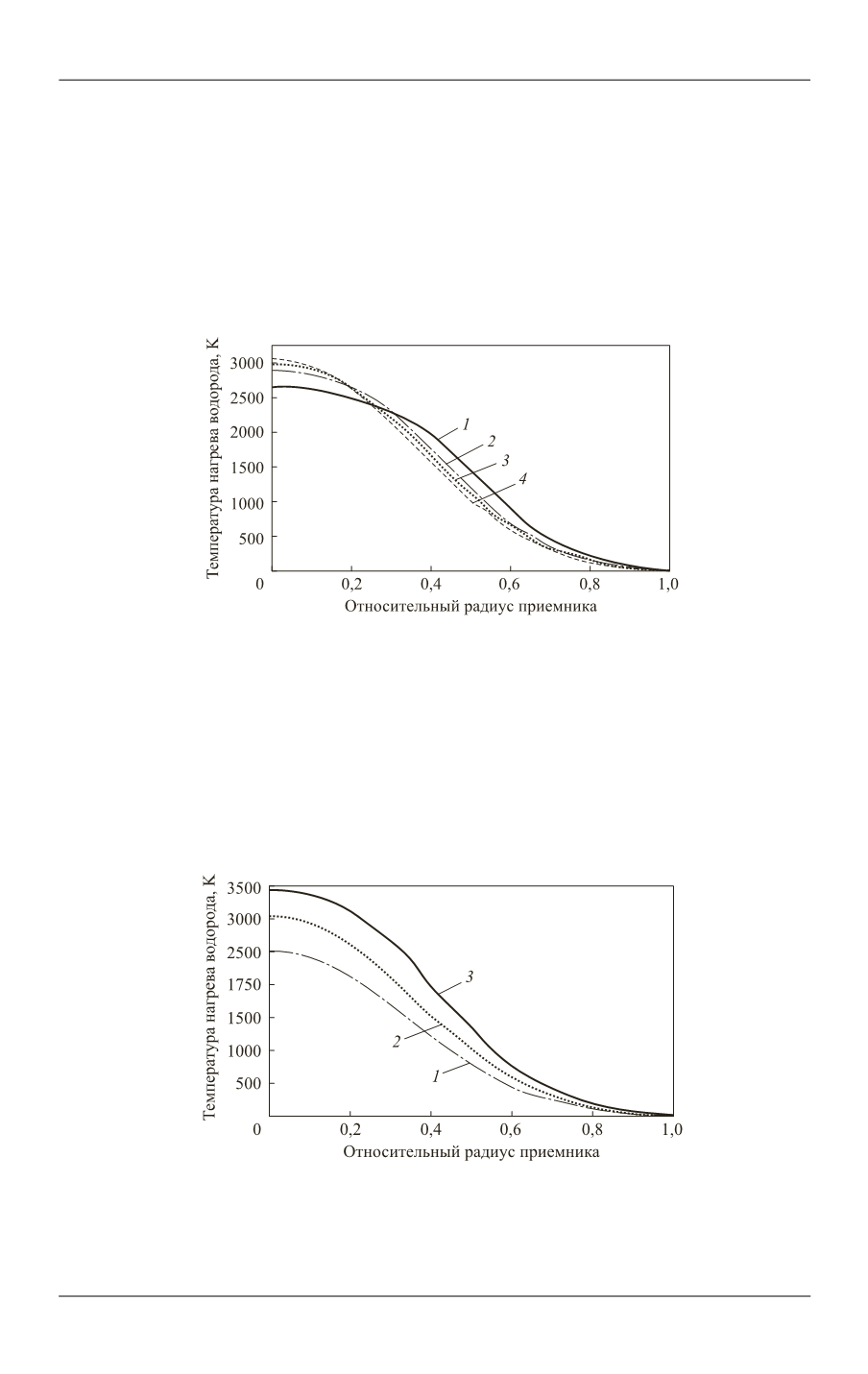
На рис. 2 приведены результаты численного интегрирования уравнения (1)
для случая нагрева водорода до 3 000 K в достаточно широком диапазоне значе-
ний параметра
, характерных для СТРкД (целесообразных для выведения
наибольшей массы полезной нагрузки (ПН) [10, 11]).
Рис. 2.
Зависимость температуры нагрева водорода от относительного радиуса приемника
для различных значений параметра точности концентратора
:
1
— Δ
= 1,5
;
2
— Δ
= 1
;
3
— Δ
= 0,75
;
4
— Δ
= 0,5
Отметим, что при больших величинах
форма распределения нарастания
температуры по относительному радиусу приемника меняется несущественно,
смещаясь лишь по оси ординат вниз в соответствии с падением уровня точно-
сти зеркала. Для различных температур нагрева эпюры распределения подобны
(рис. 3). Можно отметить схожесть зависимостей на рис. 1, 2 и 3. Поскольку те-
Рис. 3.
Распределение температуры водорода в зависимости от относительного радиуса
приемника для разных заданных температур нагрева; параметр точности концентратора
= 0,5
:
1
—
Т
= 2 500 K;
2
—
T
= 3 000 K;
3
—
T
= 3 500 K
















