
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. «Машиностроение». 2016. № 3
103
Для численного моделирования проникания сегментированных и те-
лескопических ударников использовали вычислительный алгоритм
[5, 13, 14], основанный на методе свободных лагранжевых точек [15] и
реализованный в разработанном в МГТУ им. Н.Э. Баумана программном
комплексе численного решения задач физики взрыва и удара ЭРУДИТ
(Эвристический расчет упорядоченного движения индивидуальных то-
чек). Используемый вычислительный метод был апробирован при реше-
нии широкого круга задач взрывного и ударного нагружения сплошных
сред (в том числе и задач высокоскоростного проникания ударников в
различные преграды) и хорошо себя зарекомендовал [16–18]. К числу его
достоинств следует отнести возможность расчета движений сплошной
среды с большими деформациями без использования специальных про-
цедур перестройки расчетной сетки.
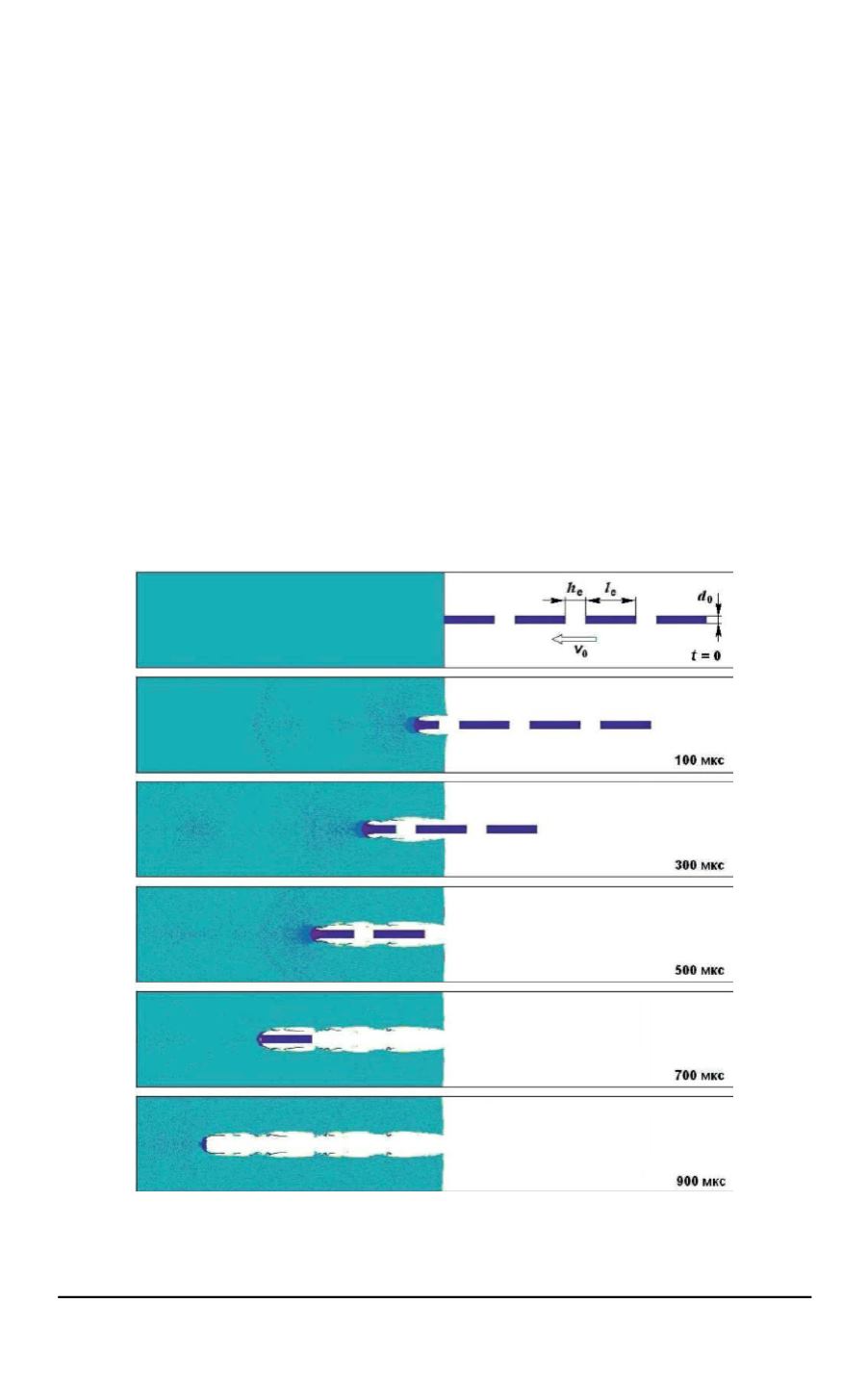
Увеличение глубины каверны, образующейся в прочной среде при
проникании удлиненного ударника в гидродинамическом режиме, мо-
жет быть достигнуто путем разделения (сегментирования) ударника на
отдельные элементы, движущиеся последовательно на некотором уда-
лении (разнесении) друг за другом (рис. 1). Авторами [19] был прове-
Рис. 1.
Проникание сегментированного ударника в стальную преграду при
начальной скорости
0
v
1400 м/с (число элементов
e
n
4; длина элемента
e
l
125 мм; разнесение
e
h
50 мм)
















