
(
Q
— объемный расход воздуха). Способ определения характеристики
потерь давления описан в работе [3].
Численное решение системы уравнений движения вязкой жидкости
в соответствии с поставленными граничными условиями основано на
алгоритме SIMPLE и (
k
–
ε
)-
модели турбулентности [4].
На расчетную область накладывались следующие начальные и гра-
ничные условия:
•
параметры атмосферного воздуха —
Р
а
=101300
Па,
t
а
=
−
40
. . .
+
+ 40
◦
С;
•
скорость ветра с различных направлений — до 30 м/с (профиль
скорости — равномерный по высоте);
•
(для непроницаемой поверхности — стенки)
v
ст
= 0
, логарифми-
ческий профиль скорости у поверхности;
•
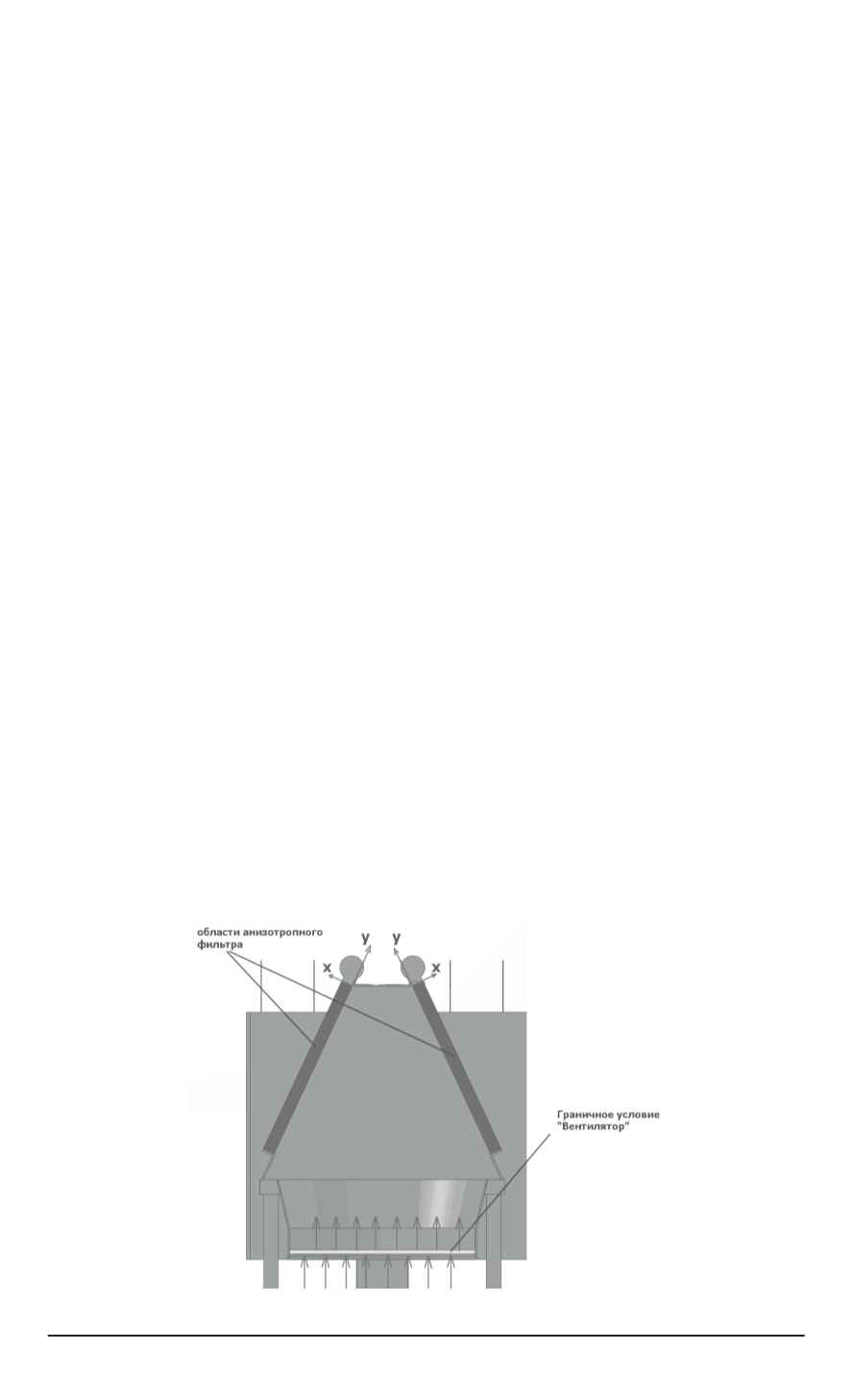
на область каждого оребренного трубного пучка — анизотроп-
ный фильтр с особыми свойствами в направлении оси
x
локальной
системы координат (рис. 3). Гидравлическое сопротивление каждого
анизотропного фильтра в направлении оси
x
задавалось в соответ-
ствии с предварительно полученной его гидравлической характери-
стикой [1]
Δ
p
ф
=
f
(
v
н
)
, где
v
н
— локальная скорость набегающего
потока. В направлении осей
y
и
z
локальных систем координат (см.
рис. 3) — гидравлическое сопротивление фильтров принималось бес-
конечно большим;
•
работа каждого вентилятора ВКУ задавалась его напорной ха-
рактеристикой
Δ
p
c
=
f
(
Q
в
)
(
Q
в
— объемный расход воздуха через
вентилятор);
•
на граничные поверхности расчетной области задавались либо
условие свободного выхода потока, либо значение нормальной скоро-
сти ветра в соответствии с расчетным режимом.
Расчетная область размером 140
×
110
×
56 м, имеющая форму па-
раллелепипеда, была разбита базовой сеткой 90
×
68
×
75 ячеек (рис. 4).
Рис. 3. Граничные условия “анизотропный фильтр” и “вентилятор”
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 1 111

















