
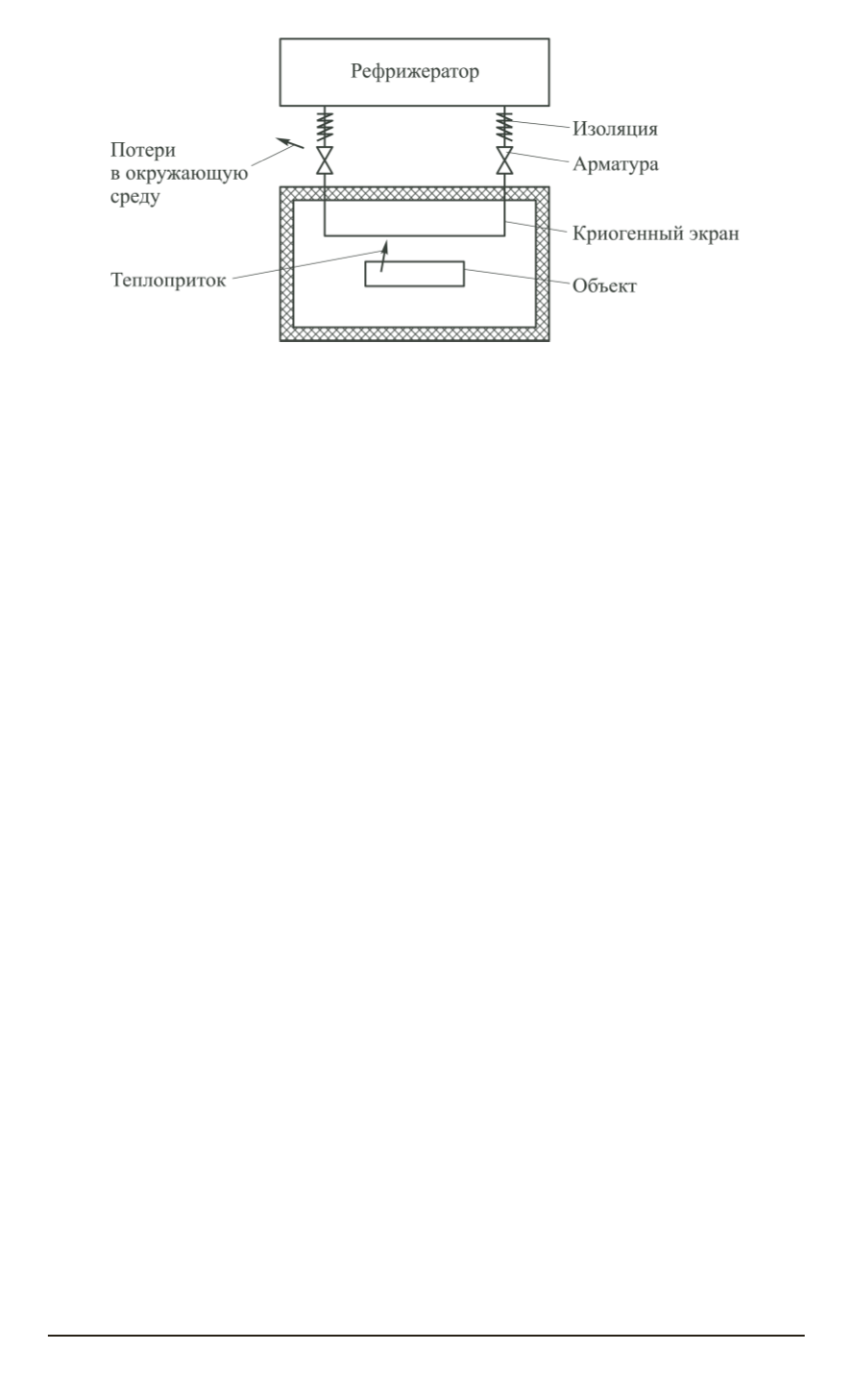
Рис. 1. Моделируемая система тепловакуумных испытаний космической
техники
Поэтому нужно заранее планировать тепловые испытания для
предварительной оценки потребных мощностей и времени охлажде-
ния. Данная задача может быть решена с помощью математического
моделирования тепловых испытаний, которое позволит оценить затра-
ты энергии на охлаждение объекта, время выхода системы на режим
для различных конструктивных решений испытательного стенда и
выбрать из них оптимальные.
Для моделирования была использована система (рис. 1), состоя-
щая из рефрижератора и вакуумной камеры, в которой размещен объ-
ект испытания и криогенный экран. К экрану подается рабочее веще-
ство — жидкий азот или жидкий гелий, получаемый в рефрижераторе-
ожижителе. Теплота в системе передается излучением. Модель учи-
тывает влияние тепловых потоков из окружающей среды, от объекта,
тепловые потери в магистралях. При моделировании работы подоб-
ных систем необходимо определить размеры и положение криоген-
ного экрана, необходимую мощность рефрижератора-ожижителя, воз-
можность достижения заданных температур на поверхности объекта.
Размеры объекта, его тепловыделения и температурный режим опре-
деляются назначением испытаний. Основная задача моделирования —
снижение температур объекта до значения, заданного в программе ис-
пытаний.
Задача математического моделирования теплообмена излучением
осложняется геометрией поверхностей источника излучения (объекта
охлаждения) и приемника излучения (криогенного экрана), а также
возможностью их различного пространственного размещения относи-
тельно друг друга [8]. Поэтому при построении модели теплообмена
между объектом и криоэкраном их поверхности предполагались стро-
го прямоугольной формы. Согласно закону Ламберта [9] количество
лучистой энергии в единицу времени
dQ
φ
пропорционально значе-
нию пространственного угла
ϕ
, в который происходит излучение, и
относительному углу наклона источника
β
1
и приемника
β
2
. Для двух
58 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 1

















