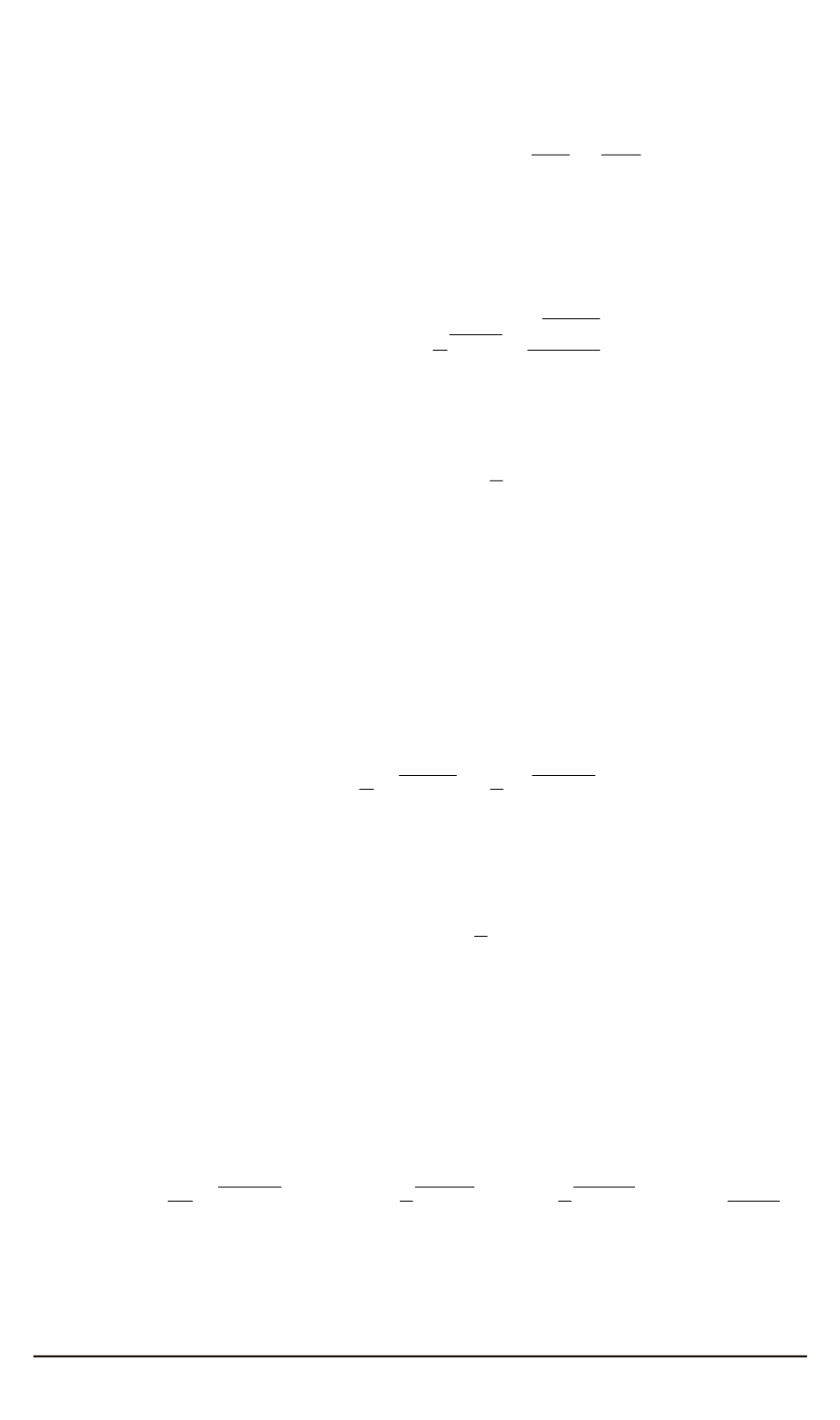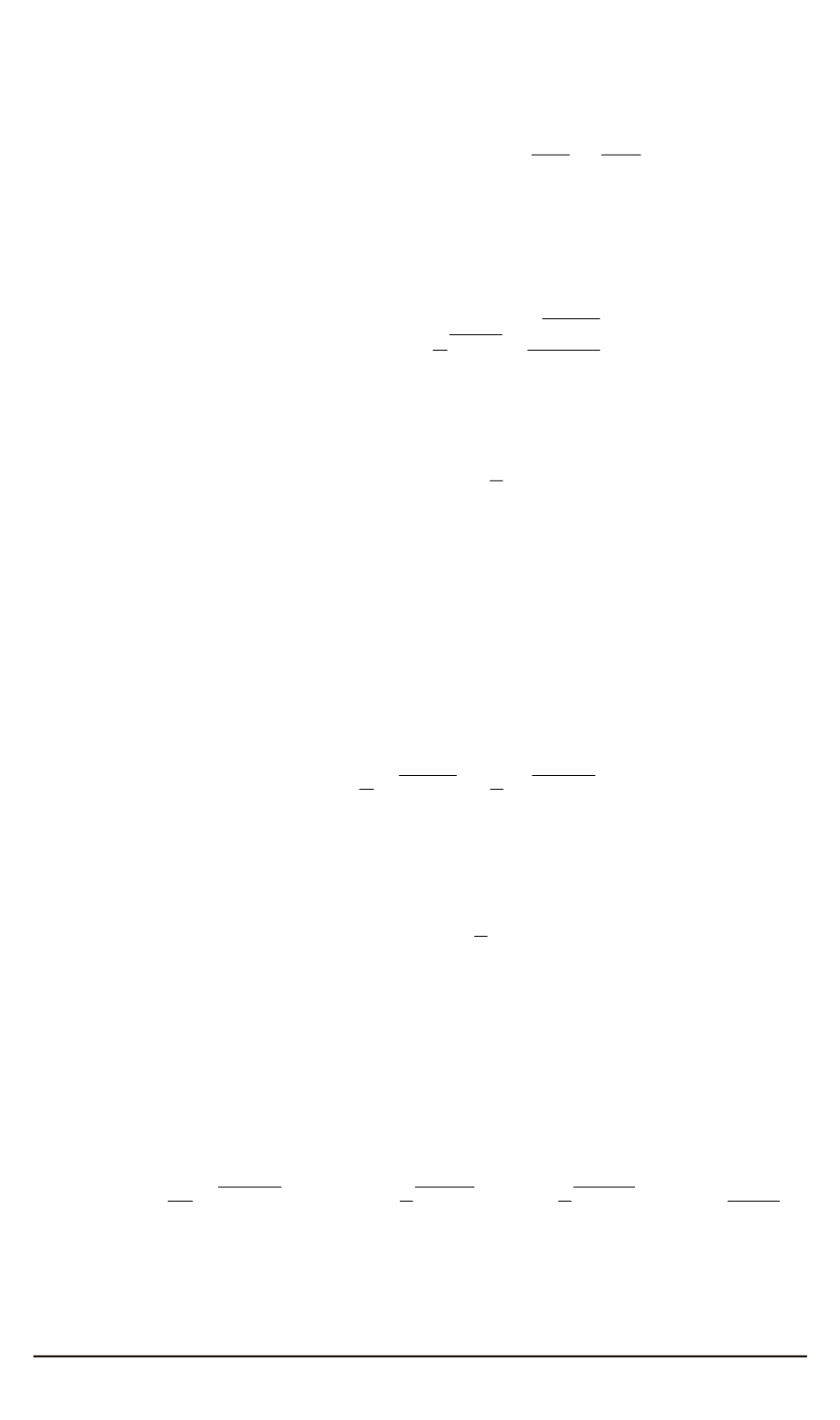
Для замыкания полученной системы уравнений необходимо вы-
полнить моделирование диссипативного, перераспределительного и
диффузионного членов. Для диффузионного члена в общем случае
полагается, что значение тройной корреляции скорости является до-
минирующим по сравнению с комплексами
v
0
p
0
и
u
0
p
0
, т.е. ими мож-
но пренебречь. Наиболее простым способом моделирования тройной
корреляции является метод градиентной диффузии, в этом случае, ис-
пользуя модель [6], член
D
ijk
в анизотропном виде можно выразить
следующим образом:
D
ijk
=
νδ
kl
+
C
s
k
ε
u
k
0
u
0
l
∂u
i
0
u
j
0
∂x
l
,
где
C
s
= 0
,
22
.
Диссипативный член моделируется, основываясь на гипотезе об
изотропности малых вихрей, тогда
ε
ij
=
2
3
δ
ij
ε
.
Перераспределительный член является наиболее сложным для мо-
делирования, в литературе существует множество вариантов, предло-
женных разными исследователями. В настоящей работе использована
модель Гибсона – Лаундера [7]. В этом случае перераспределительный
член записывается в виде суммы трех слагаемых:
Φ
ij
= Φ
ij,
1
+ Φ
ij,
2
+
+ Φ
ij,
3
, где
Φ
ij
1
— слагаемое, не зависящее от производной скорости,
также называемое “медленным” слагаемым, или слагаемым Ротта, ко-
торый предложил следующую форму записи:
Φ
ij,
1
=
−
ρ
С
1
ε
k
u
i
0
u
j
0
−
1
3
δ
ij
u
k
0
u
k
0
.
Второе слагаемое, называемое “быстрым” или “быстрое деформи-
рование”, в соответствии с [8] записывается следующим образом:
Φ
ij,
2
=
−
С
2
P
ij
−
1
3
δ
ij
P
kk
.
Третье слагаемое называется “отражение стенки” и является необ-
ходимым в окрестностях стенок, так как служит для предотвращения
изотропизации турбулентности, вызванной слагаемыми
Φ
ij
1
+ Φ
ij
2
:
Φ
ij,
3
= Φ
ijw
1
+ Φ
ijw
2
.
Согласно [9] первое слагаемое можно записать в виде
Φ
ijw
1
=
C
1
w
ρε
k
u
k
0
u
0
m
n
k
n
m
δ
ij
−
3
2
u
i
0
u
k
0
n
j
n
k
−
3
2
u
j
0
u
k
0
n
i
n
k
l
2
,
5
l
n
,
где
n
= (
n
i
, n
j
, n
k
)
— единичный вектор, нормальный к поверхности
стенки;
l
n
— расстояние до стенки;
l
— масштаб турбулентности, рав-
ный
l
=
k
3
/
2
/ε
.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2014. № 3 27