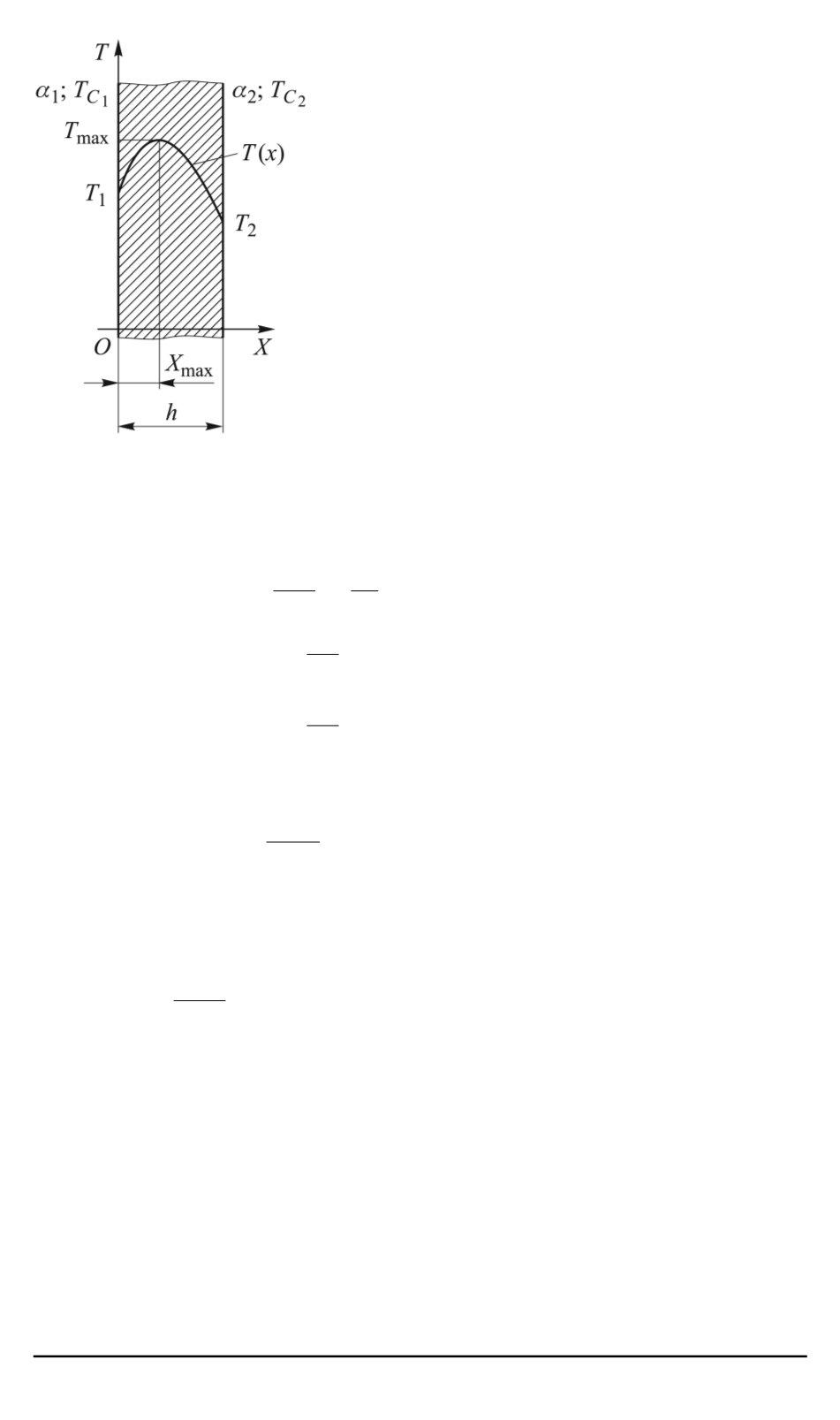
К расчету температурного
поля в пластине с равномер-
но распределенными источ-
никами теплоты
сторон находится в условиях конвективно-
го теплообмена с внешней средой (рису-
нок). Заданы температуры
T
c1
и
T
c2
среды и
коэффициенты теплоотдачи
α
1
и
α
2
с обе-
их сторон пластины; объемная плотность
внутренних источников теплоты
q
V
, тепло-
проводность материала
λ
и толщина пла-
стины
h
. Необходимо определить темпера-
турное поле в пластине
T
=
T
(
x
)
, коорди-
нату температурного максимума
x
max
и зна-
чение максимальной температуры, а также
плотность тепловых потоков
q
1
и
q
2
через
внешние поверхности пластины.
Сформулируем математическую модель
задачи:
d
2
T
dx
2
+
q
V
λ
= 0;
(39)
−
λ
dT
dx
x
=0
=
−
α
1
(
T
1
−
T
c1
);
(40)
−
λ
dT
dx
x
=
h
=
α
2
(
T
2
−
T
c2
)
(41)
и ее аналог в безразмерном виде:
d
2
Θ
dξ
2
+
Po
= 0;
(42)
Θ
0
(
ξ
1
−
Bi
1
Θ
1
) =
−
Bi
1
Θ
c1
;
(43)
Θ
0
(
ξ
2
+
Bi
2
Θ
2
) =
Bi
2
Θ
c2
,
(44)
где Po
=
q
V
h
2
λT
m
; Bi
1
=
α
1
h/λ
; Bi
2
=
α
2
h/λ
;
Θ
c1
=
T
c1
/T
m
;
Θ
c2
=
T
c2
/T
m
;
ξ
=
x/h
.
Сравнив уравнения (42)–(44) с уравнениями (15)–(17) обобщенной
модели, получим
b
ξ
=
c
(
ξ
) = 0;
F
(
ξ
) =
Po
=
const
;
γ
1
=
γ
2
= 1;
β
1
=
−
Bi
1
;
β
2
=
Bi
2
;
f
1
(
Fo
) =
−
Bi
1
Θ
c1
;
f
2
(
Fo
) =
Bi
2
Θ
c2
.
(45)
Далее, используя выражения (45), формулы таблицы и формулы
(27), (28), (30)–(35), получим
54 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2014. № 1


