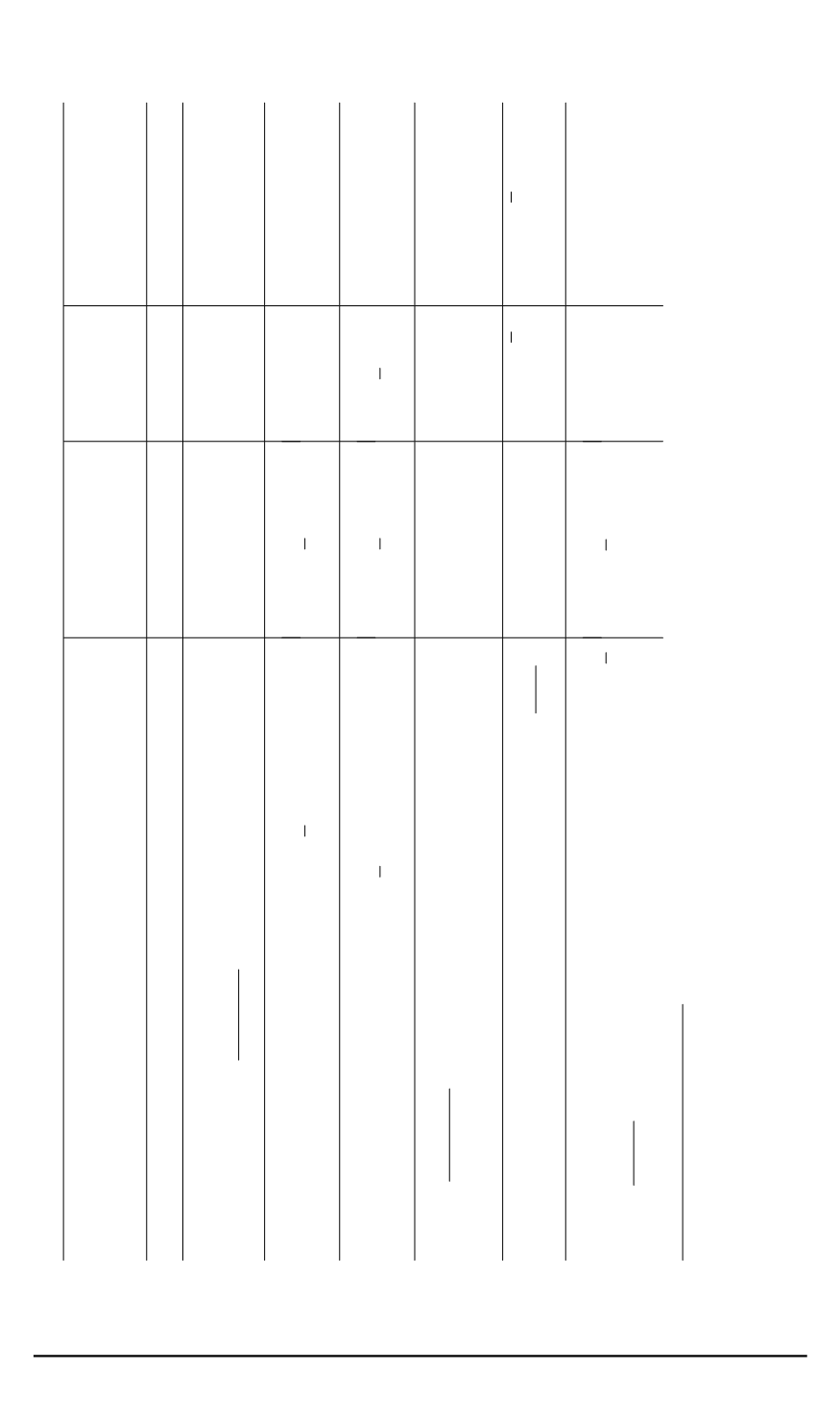
Параметры математической модели тел простой геометрической формы
Форма тела и коэффициенты в уравнении (15)
Однородное
уравнение
теплопроводности
Функция
ψ
(
ξ
)
Функция
ϕ
(
ξ
)
Пластина:
b
ξ
=
c
ξ
= 0
Θ
00
= 0
ξ
1
Пористая пластина, охлаждаемая жидкостью:
c
ξ
= 0
,
b
ξ
=
Кп
=
−
˙
mc
p
ж
l
λ
к
(1
−
Π)
Θ
00
−
Кп
Θ
0
= 0 exp(
Кп
ξ
)
1
Полый или сплошной цилиндр:
c
ξ
= 0
,
b
ξ
=
1
ξ
Θ
00
+
1
ξ
Θ
0
= 0
ln
ξ
1
Сплошной или полый шар:
c
ξ
= 0
,
b
ξ
=
2
ξ
Θ
00
+
2
ξ
Θ
0
= 0
1
ξ
1
Ребро (стержень) постоянного сечения:
c
ξ
=
−
(
ml
)
2
,
b
ξ
= 0
,
m
=
p
α
Π
/
(
λS
0
)
(
Π
, S
0
— периметр и площадь поперечного се-
чения стержня)
Θ
00
−
(
ml
)
2
Θ
0
= 0 exp(
−
mlξ
)
exp(
mlξ
)
Ребро треугольного и трапецевидного поперечного сечения
с малым углом при вершине:
c
ξ
=
−
(
ml
)
2
,
b
ξ
= 1
,
m
=
p
α/λδ
ξ
Θ
00
+ Θ
0
−
−
(
ml
)
2
Θ = 0
I
0
(2
ml
√
ξ
)
K
0
(2
ml
√
ξ
)
Круглое ребро постоянной толщины
2
δ
:
c
ξ
=
−
(
ml
)
2
,
b
ξ
=
1
ξ
,
m
=
p
α/
(
λδ
)
Θ
00
+
1
ξ
Θ
0
−
−
(
ml
)
2
Θ = 0
I
0
(
mlξ
)
K
0
(
mlξ
)
П р и м е ч а н и е.
I
0
,
K
0
— модифицированные функции Бесселя первого и второго рода нулевого порядка [8–10]
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2014. № 1 51


