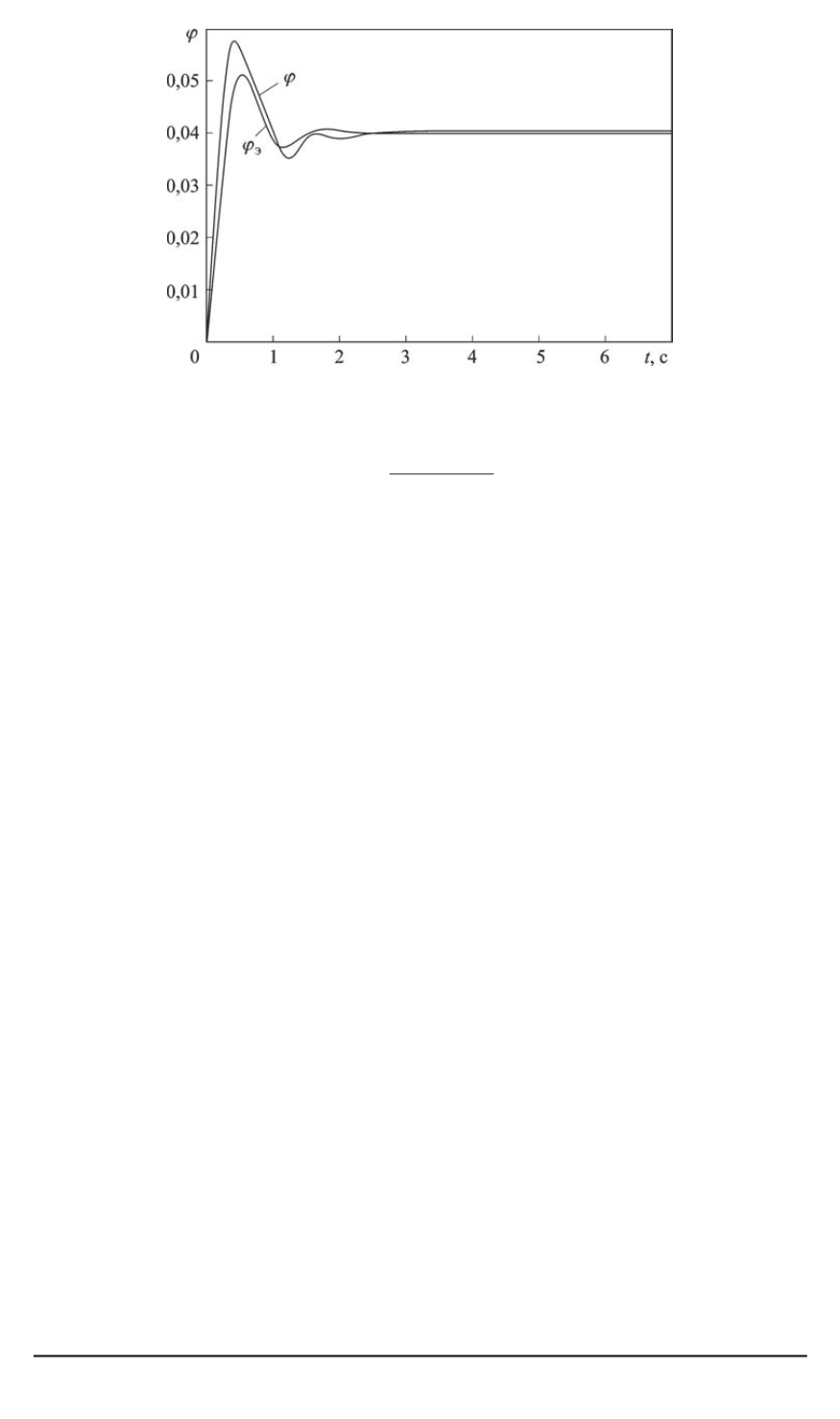
Рис. 3. Графики переходных процессов
ϕ
(
t
)
,
ϕ
э
(
t
)
при
ζ
г
=
−
1
,
π
0
= 0
,
ψ
= 0
При вычислении параметров использовалась евклидова норма кри-
терия оптимальности (5)
J
(p) = E (p) =
l
k
=1
e
2
k
(p)
→
min
p
= 0
,
0792
,
(6)
где e
k
(p)
— элементы вектора
E (p)
. В качестве ОНБ использовались
256 функций Уолша, упорядоченных по Адамару. При поиске мини-
мума целевой функции (6) использовался метод Гаусса–Ньютона, при
этом понадобилось 8 итераций (начальные приближения параметров
равнялись единице).
Следует отметить, чтодля успешногорешения задачи параметри-
ческого синтеза необходимо изучить динамику поведения объекта без
системы регулирования на начальном этапе ее функционирования и
учесть ее при выборе эталонного переходного процесса. Это вызвано
инерционностью не только самого объекта, но и, в первую очередь,
гидравлической части системы регулирования. Поскольку метод ис-
пользует аппарат математического программирования, то можно на
искомые значения параметров регулирования наложить ограничения,
связанные с их физической реализуемостью.
Анализ результатов показывает, что проекционно-матричный ме-
тод может успешно применяться при расчете систем регулирования
энергетических турбин, динамика которых описывается нелинейными
дифференциальными уравнениями, чтопозволяет уже на этапе проек-
тирования учитывать все более “тонкие” конструктивные особенности
конкретного турбоагрегата без какого-либо упрощения.
Работа была выполнена при финансовой поддержке Российского
фонда фундаментальных исследований и Правительства Калужской
области (грант № 12-01-97520).
ЛИТЕРАТУРА
1.
Калашников А.А.
Динамика регулирования турбин. М.: Энергоатомиздат, 1999.
328 с.
52 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2013. № 4


