
А.С. Морозов, А.С. Кротов, С.И. Каськов
54
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2016. № 5
Анализ изменения холодильного коэффициента.
На рис. 3 видно, что при
достаточно низких значениях
z
холодильный коэффициент принимает отрица-
тельные значения, что, на первый взгляд, кажется нефизичным. Однако этому
можно дать объяснение. При выводе формулы для
max
предполагалось, что
температуры спаев жестко фиксированы, а сам коэффициент определялся как
функция от силы тока следующим образом:
2
1,2
1
2
1 2 0 1
1
2
,
I I R K T
Q
W
T T I I R
где
1,2
1 2 1
T
— коэффициент Пельтье;
K
— термическое сопротивле-
ние в контуре с током.
Мощность
,
W
затрачиваемая на преодоление эффекта Зеебека
1 2 0 1
з
Q
T T I
и теплоту Джоуля
2
дж
Q I R
, по определению не может
быть отрицательной. Следовательно, отрицательное значение принимает теп-
лота
1
Q
, т. е. теплота отводится от холодного спая, хотя цель холодильной ма-
шины обратная.
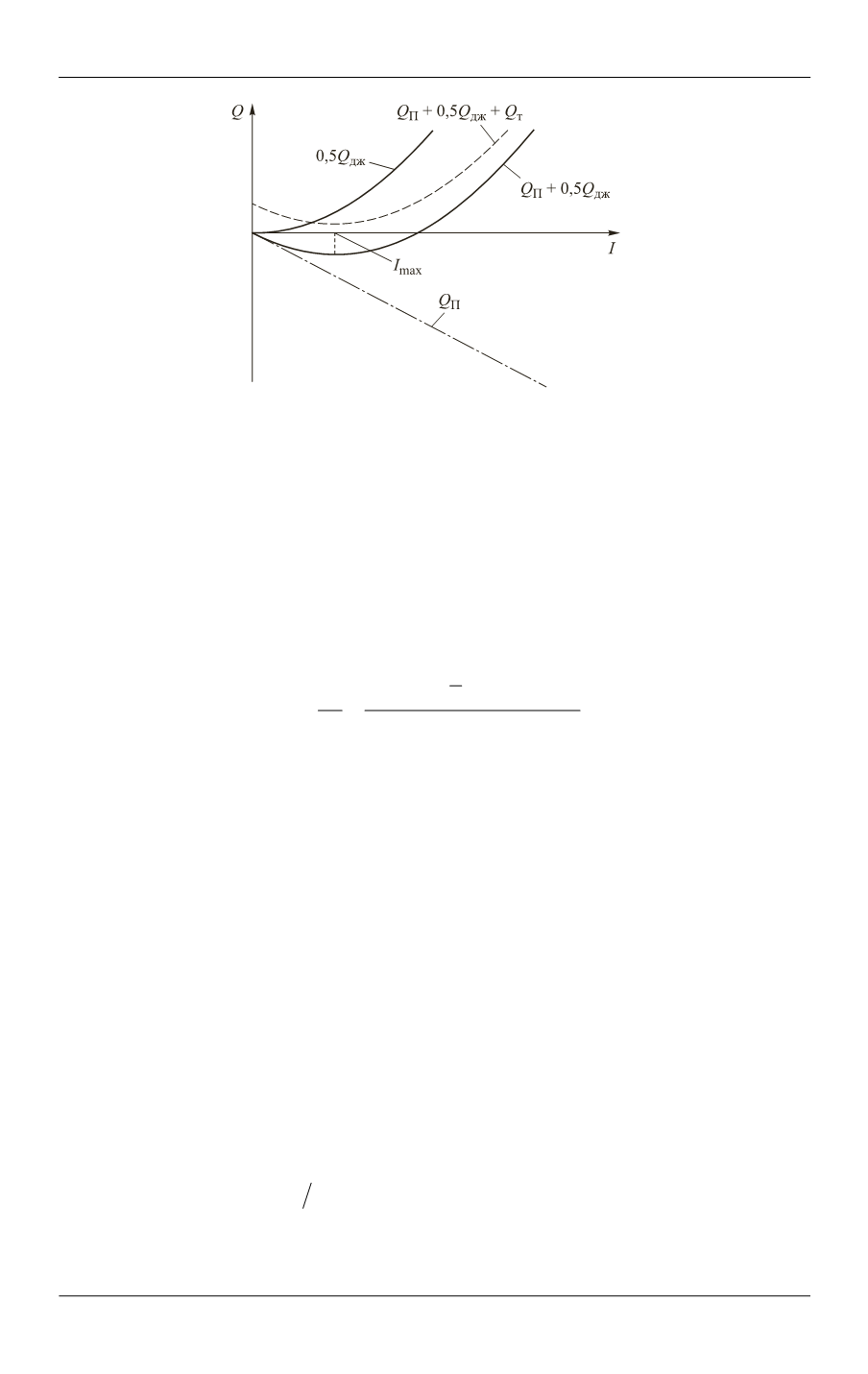
Анализируя
1
Q
(см. рис. 5), выявили следующее: эффект охлаждения чув-
ствительного элемента (подвод теплоты к холодному спаю) реализуется за счет
теплоты Пельтье
1,2
,
Q I
пропорциональной силе тока. Но в то же время на
холодном спае выделяется джоулева теплота, пропорциональная квадрату силы
тока и уменьшающая требуемый эффект охлаждения. В первом приближении
принято считать, что на холодном спае выделяется половина джоулевой теплоты
всего контура с током
2
0,5 .
I R
Очевидно, что линейная функция до некоторого
значения тока
max
1,2
I
R
растет быстрее, чем параболическая, и поэтому в
рамках данной модели (при пренебрежении эффекта Томпсона и теплопроводно-
сти внутри контура с током) холодопроизводительность будет достигать своего
Рис. 5.
График зависимости теплоты
0
Q
от силы тока
















