где
{
v
}
— полный вектор обобщенных координат, учитывающий все пере-
мещения всех узлов модели;
{
V
}
— полный вектор сил, действующих вдоль
компонент
{
v
}
,
[
L
]
— матрица жесткости физической модели, соответству-
ющая полному вектору обобщенных координат
{
v
}
.
Матрица
[
L
]
формируется из матриц жесткости КЭ:
[
L
] =
X
n
([
T
]
т
∙
[
K
]
∙
[
T
])
,
(2)
где
n
— число КЭ модели;
[
K
]
— матрица жесткости КЭ в собственной,
локальной системе координат;
[
T
]
— матрица преобразования обобщенных
координат КЭ в локальной системе координат в глобальную (в систему обоб-
щенных координат модели).
Для описания динамических процессов, протекающих в агрегатах СС, ис-
пользовалась система дифференциальных уравнений, представляющая собой
уравнение динамического равновесия модели агрегата стартового комплекса:
[
M
]
∙ {
q
00
}
+
α
∙
[
L
]
∙ {
q
0
}
+ [
L
]
∙ {
q
}
=
=
−
g
∙
[
M
]
∙ {
ε
}
+ Σ
{
P
} ∙
u
(
t
) + Σ
{
Φ
R
} ∙
R
(
х
, x
0
)
,
(3)
где
{
q
}
,
{
q
0
}
,
{
q
00
}
— векторы перемещений, скоростей и ускорений узлов
модели в направлении обобщенных координат;
[
M
]
и
[
L
]
— приведенные
матрицы масс и жесткости модели;
α
— коэффициент, учитывающий рассея-
ние энергии за счет внутреннего демпфирования;
g
— ускорение свободного
падения;
{
ε
}
— вектор направления гравитационных сил;
{
P
}
— вектор рас-
пределения внешних сил;
u
(
t
)
— функция изменения вектора внешних сил
во времени;
{
Φ
R
}
— вектор, определяющий положение нелинейной связи
в пространстве;
R
(
х
0
)
— характеристика нелинейных связей;
x
— удлинение
связи, зависящее от
{
q
}
;
{
x
0
}
— скорость удлинения связи, зависящая от
{
q
0
}
.
После решения уравнений (1) и (3) были определены перемещения, ско-
рости и ускорения характерных точек модели. На основе полученных данных
с помощью методики, приведенной в работе [6], были определены внутрен-
ние силовые факторы и напряжения в КЭ моделей агрегатов СС и определены
коэффициенты запаса по прочности.
Физическое моделирование и расчетный анализ отводимых агрегатов СС
проводился с помощью программного комплекса SADAS, созданного на ка-
федре “Стартовые ракетные комплексы” МГТУ им. Н.Э. Баумана.
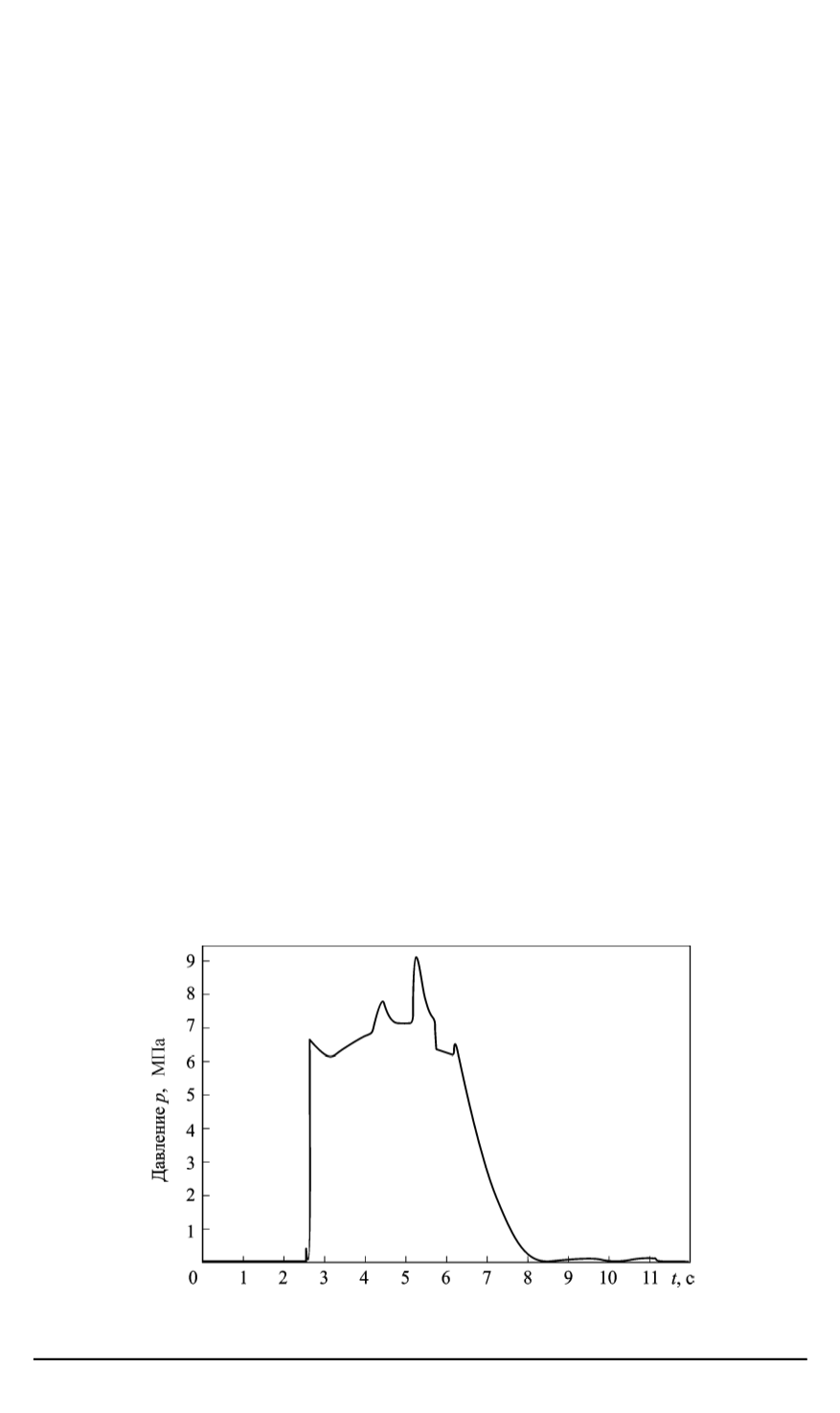
Рис. 4. Результаты расчета изменения давления в гидробуфере (см. рис. 1) при
торможении кабель-заправочной мачты СС для РН “Союз-2”
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2011. № 1 35


