часть четвертого уравнения системы (1) учитывает влияние подогрева
жидкости и газа на значения параметров потока, причем
f
(
k
)
— функ-
ционал от местного значения показателя изоэнтропы, определяемый
для зоны смешения жидкость–воздух с помощью уравнения Дальто-
на [6],
dQ
dt
— скорость подвода и выделения теплоты в расчетной зоне.
Система уравнений сохранения замыкается уравнением состояния в
виде эмпирической адиабаты Тейда, где
с
= 3200
∙
10
5
Па,
k
= 7
,
15
.
В качестве граничных условий на жестких стенках полостей фор-
сунки использовалось условие равенства нулю нормальной к поверх-
ности составляющей массовой скорости потока
w
= 0
, а начальных
условий газодинамических параметров — параметры невозмущенной
стандартной атмосферы при показателе изоэнтропы воздуха
k
в
= 1
,
4
.
В струе жидкости значение показателя изоэнтропы жидкости состав-
ляет
k
ж
= 7
,
15
и давление в ней
P
ж
= 250
Па.
Систему уравнений (1) решали конечно-разностным методом вто-
рого порядка точности типа “предиктор-корректор” с использованием
трехточечного сглаживания [9]. В процессе расчетов контролировали
точность решения по энтропии. Достоверность разработанной мето-
дики проверяли путем сравнения полученных результатов расчетов
зависимости давления
p
(
t
)
с аналогичными зависимостями
p
(
t
)
, полу-
ченными экспериментально.
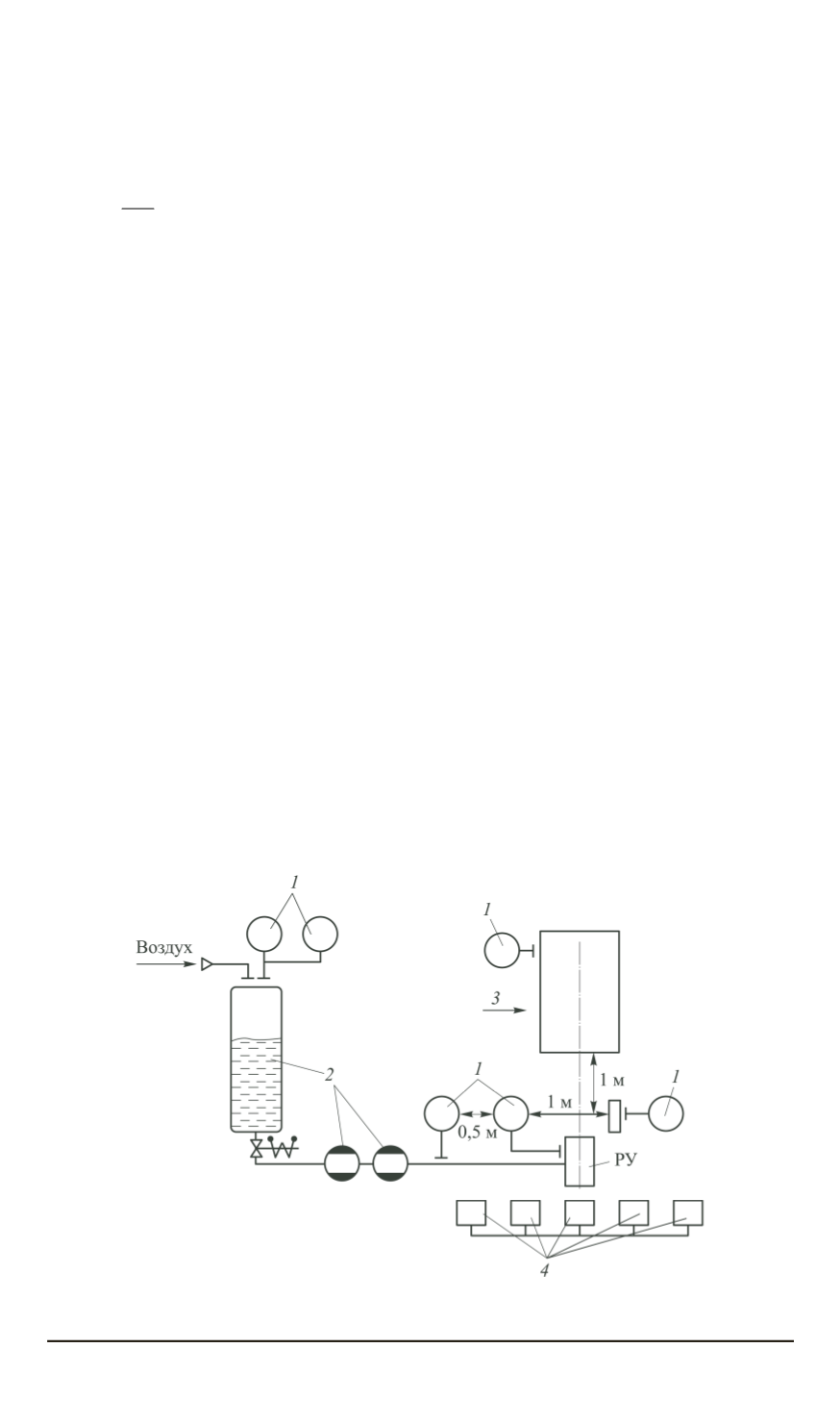
Экспериментальные исследования
процесса функционирования
пленочных форсунок проводились на специальном стенде, схема ко-
торого показана на рис. 1, а схема конструкции форсунки — на рис. 2.
Канал форсунки имеет постоянные линейные размеры и является ще-
левым.
Рис. 1. Стенд для продувок моделей распыляющих устройств
36 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2014. № 5


