Таким образом, вариационная задача сводится к решению двухто-
чечной краевой задачи для системы дифференциальных уравнений (2),
(9) с учетом выражений (6), (7), (10) при заданных граничных условиях
(4) и (5). Конечные значения сопряженных переменных определяются
из условия трансверсальности.
Для решения двухточечной краевой задачи использовали метод по-
следовательных приближений [3].
Решение задачи оптимизации позволяет определить минимальное
значение суммарного характеристического импульса
∆
V
хар
при дан-
ных начальных условиях для всех моделей атмосфер. В результате
решения была определена программа оптимального управления аэро-
динамическим качеством КА, которая представляет собой релейную
функцию с однократным переключением с отрицательного на поло-
жительное значение.
Для КА с массой
m
= 5700
кг, площадью миделя
S
= 4
,
91
м
2
и
параметрами
K
= 0
,
15
(
С
xa
= 1
,
48)
,
K
= 0
,
17
(
С
xa
= 1
,
47
),
K
= 0
,
2
(
С
xa
= 1
,
45
),
K
= 0
,
22
(
С
xa
= 1
,
43
) и
K
= 0
,
25
(
С
xa
= 1
,
39
) проведе-
но численное решение поставленной задачи. В результате определен
диапазон возможных скоростей входа
∆
V
0
и необходимое значение
суммарного характеристического импульса
∆
V
хар
для различных мо-
делей атмосферы планеты.
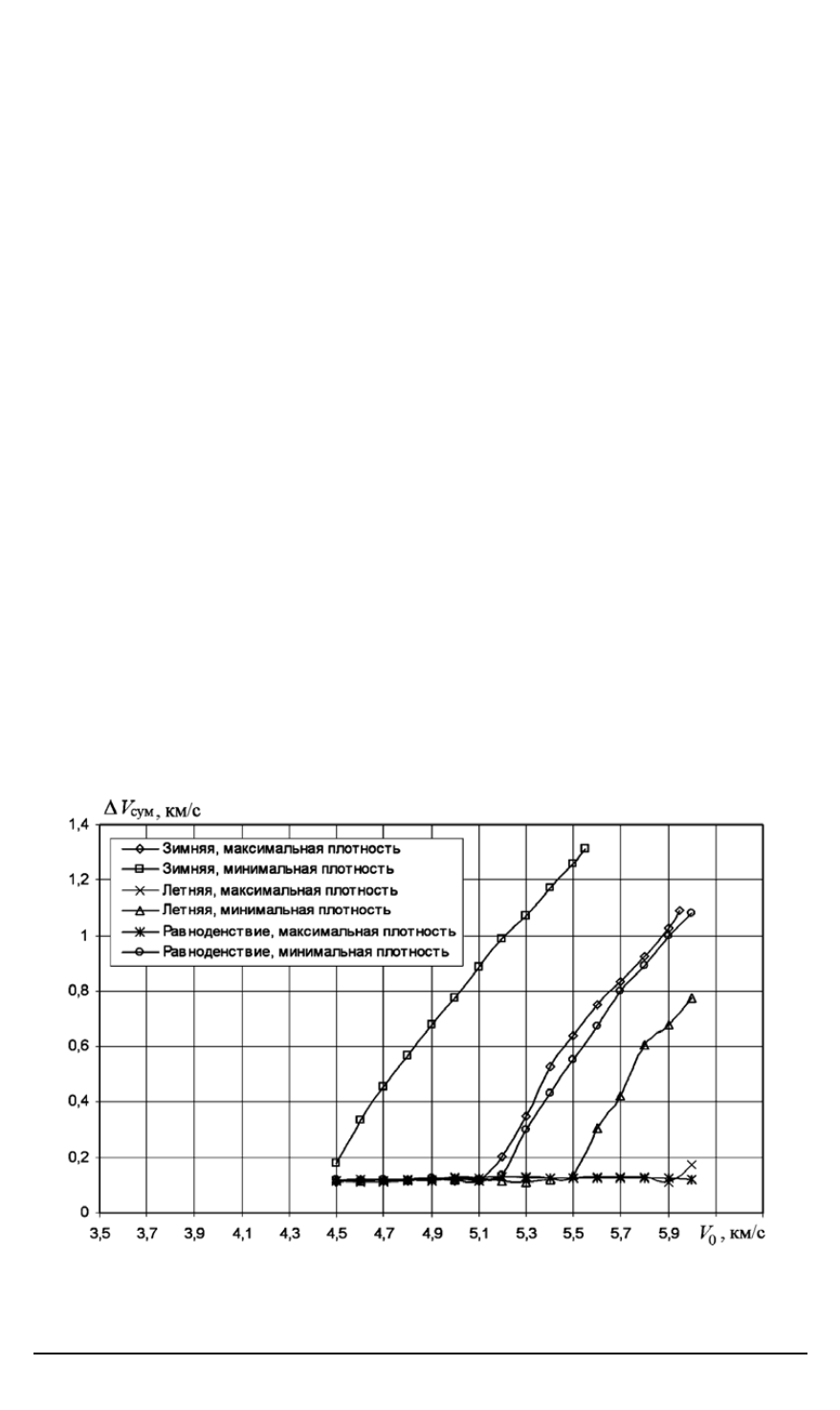
На рис. 1 приведены диапазоны возможных скоростей входа
∆
V
0
для КА со значением
K
= 0
,
15
(
С
xa
= 1
,
48
). Каждой модели атмо-
Рис. 1. Диапазон возможных скоростей входа КАсо значением
K
= 0
,
15
(
С
xa
= 1
,
48
) для различных моделей атмосферы и суммарный характеристиче-
ский импульс для выведения КАна орбиту ИСМ
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2005. № 4 7


