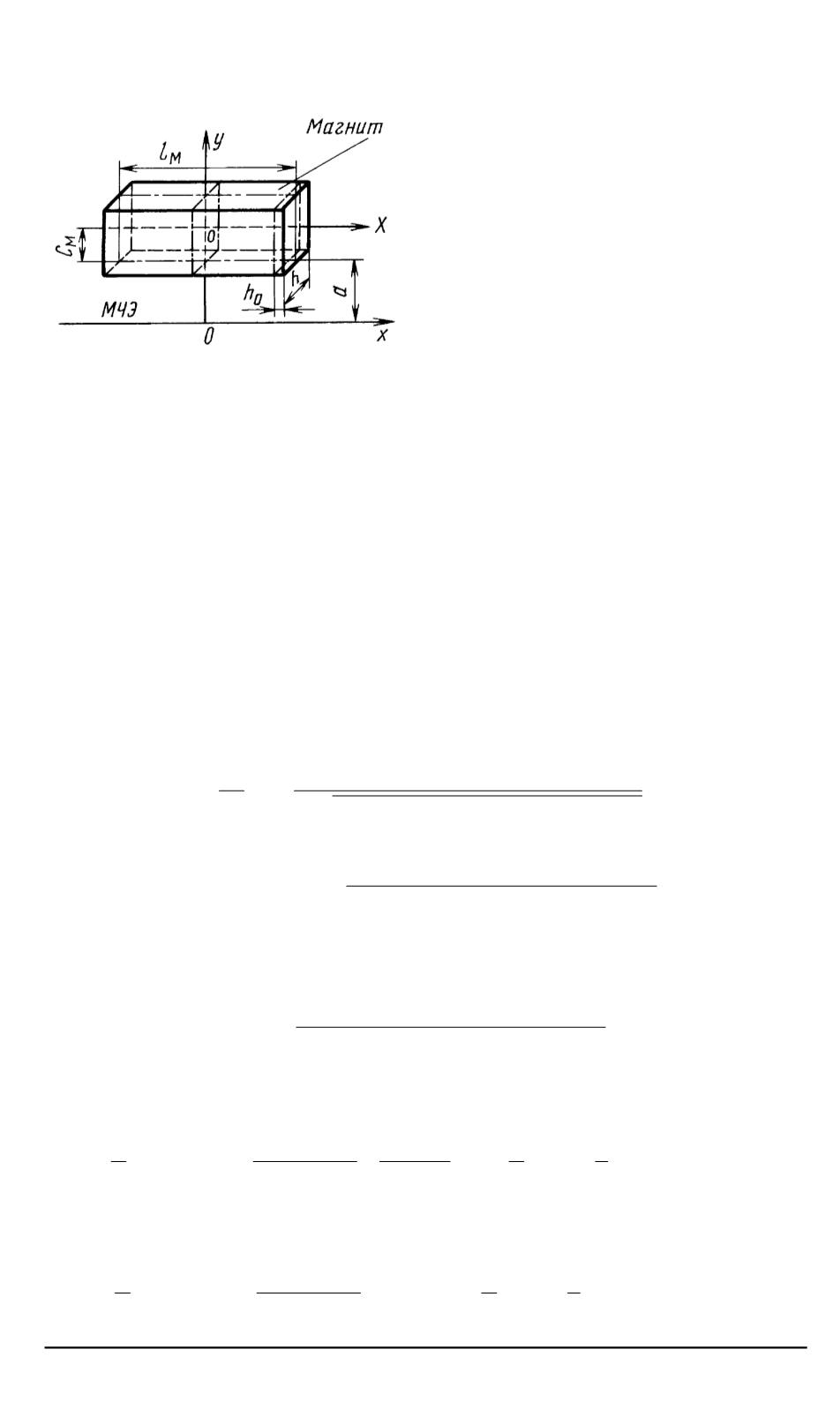
Рис
. 3.
Расчетная схема поля
H
0
по ме
-
тоду эквивалентного соленоида
пространства сигнального пре
-
образователя магнитострикцион
-
ной системы
.
Допуская
,
что намагниченность
J
M
стержневых магнитов по оси
Х
распределяется согласно зависимо
-
сти
[5]:
J
M
(
X
) =
J
s.
M
{
2
−
ch
[
k
J
(
X
−
l
M
/
2)]
}
,
можно предположить
,
что анало
-
гично распределяется эквивалент
-
ный ток по равноудаленным на шаг
h
0
виткам
i
= 1
,
2
, . . . , m
соленои
-
да
:
I
э
.
т
=
−
I
т
m
X
i
=1
{
2
−
ch
[
k
J
(
i
−
1)
h
0
−
l
M
/
2]
}
,
(
10
)
где
I
т
—
эквивалентный ток соленоида
,
создающий намагниченность
насыщения
J
s.
M
;
k
J
—
эмпирический коэффициент формы магнита
.
Тогда
,
созданная им индукция
B
0
=
B
r
(
остаточная
B
r
)
продольно
-
го магнитного поля в произвольной точке с координатами
(
а
,
х
)
про
-
странства СМП
(
РМП
),
составит величину
:
B
0
=
µ
0
H
0
=
µ
0
π
m
X
i
=1
I
э
.
т
[
X
+ (
i
−
1)
h
0
]
a
p
(
C
M
+
a
)
2
+ [
X
+ (
i
−
1)
h
0
]
2
×
½
C
1
(
C
2
M
+
a
2
) + [
X
+ (
i
−
1)
h
0
]
2
(
C
M
−
a
)
2
+ [
X
+ (
i
−
1)
h
0
]
2
−
C
2
¾
,
(11)
здесь
C
1
, C
2
—
эллиптические интегралы первого и второго порядка
аргумента
:
k
2
э
=
4
C
M
a
(
C
M
+
a
)
2
+ [
X
+ (
i
−
1)
h
0
]
2
,
которые описываются выражениями
[6]:
C
1
=
π
2
(
1
−
4
X
n
·
(2
n
−
1)!!
2
n
·
n
!
¸
k
2
n
э
2
n
−
1
)
=
π
2
½
1
−
1
2
k
2
э
−
30
k
4
э
−
. . .
¾
,
C
2
=
π
2
(
1 +
4
X
n
=1
·
(2
n
−
1)!!
2
n
·
n
!
¸
2
k
2
n
э
)
=
π
2
½
1 +
1
4
k
2
э
+ 8100
k
4
э
+
. . .
¾
.
82 ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Машиностроение
”. 2004.
№
2


